CyberGeo, No. 241, 13/06/2003

Between the Sinusoidal projection and the Werner:
an alternative to the Bonne.

Une alternative à la projection cartographique de Bonne.

Henry Bottomley

Abstract
The Sinusoidal projection and the Werner projection are equal area projections of the world. There are intermediate projections with similar properties, of which the best known is the Bonne projection. This note describes an alternative intermediate projection.

Mots-clés : projection cartographique, projection équivalente, projection sinusoïdale, Werner, Bonne

Résumé
La projection sinusoïdale et la projection de Werner sont des projections équivalentes du monde: elles conservent les surfaces. Entre les deux, il existe des projections avec des propriétés similaires, parmi lesquelles la plus connue est la projection de Bonne. Cette article represente une autre projection entre la projection sinusoïdale et celle de Werner.

Key-words : map projection, equal area projection, sinusoidal projection, Werner, Bonne

----------------------------------------------------------------------------------------------------

Both the Sinusoidal projection and the Werner provide simple equal area map projections, and have been used for many centuries. Unlike cylindrical equal area projections, they both reflect the fact that lines of latitude are shorter nearer the poles than those near the equator. To achieve this, they keep the central meridian straight and preserve distances along it, while transforming other meridians into curves; this has the effect of distorting shapes, in particular those towards the sides of the map, but helps remind the viewer of the curvature of the earth’s surface. There are intermediate projections with similar properties, of which the best known is the Bonne projection used extensively in the 19^th century. This note describes an alternative intermediate projection. Some world maps are shown, first with graticules and Tissot’s Indicatrix, and then later showing the effect of the projections on land areas.

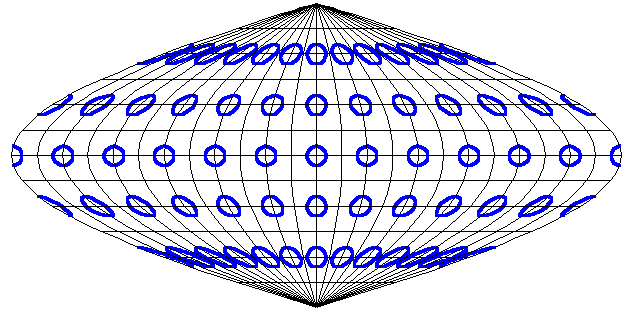
The Sinusoidal projection draws lines of latitude as parallel horizontal straight lines, with lengths equal to their lengths on the globe, and placed symmetrically and equally spaced across the vertical central meridian. The meridians, including the two representations of the antipodal meridian (the right and left sides of the map), take the form of rotated sine curves.

The Werner projection draws lines of latitude as concentric circular arcs centred on the pole, with arc lengths equal to their lengths on the globe, and placed symmetrically and equally spaced across the vertical central meridian. The two representations at the sides of the antipodal meridian come together near the North Pole, and overall the map forms a heart shape.

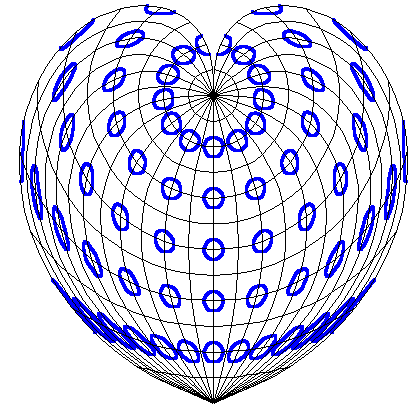
The Sinusoidal and Werner projections are similar in definition, and near the South Pole, they are similar in effect. There is a sense in which the Werner projection is a Sinusoidal projection with its right and left sides each wound upwards round the North Pole as far as is possible without the map overlapping itself. This raises the possibility of an intermediate position. One such is the Bonne projection.

The Bonne projection draws lines of latitude as concentric circular arcs, with arc lengths equal to their lengths on the globe, and placed symmetrically and equally spaced across the vertical central meridian. Unlike the Werner projection, the centre of the circular arcs is not at the North Pole; it is some distance above it on the extension of the central meridian. Changes to this distance vary the details of the projection. In the limit, this produces a Werner projection when the distance is zero, and a Sinusoidal projection when the distance approaches infinity. In the Bonne projection, the meridians form complex curves, and this is particularly noticeable at the sides for the two representations of the antipodal meridian.

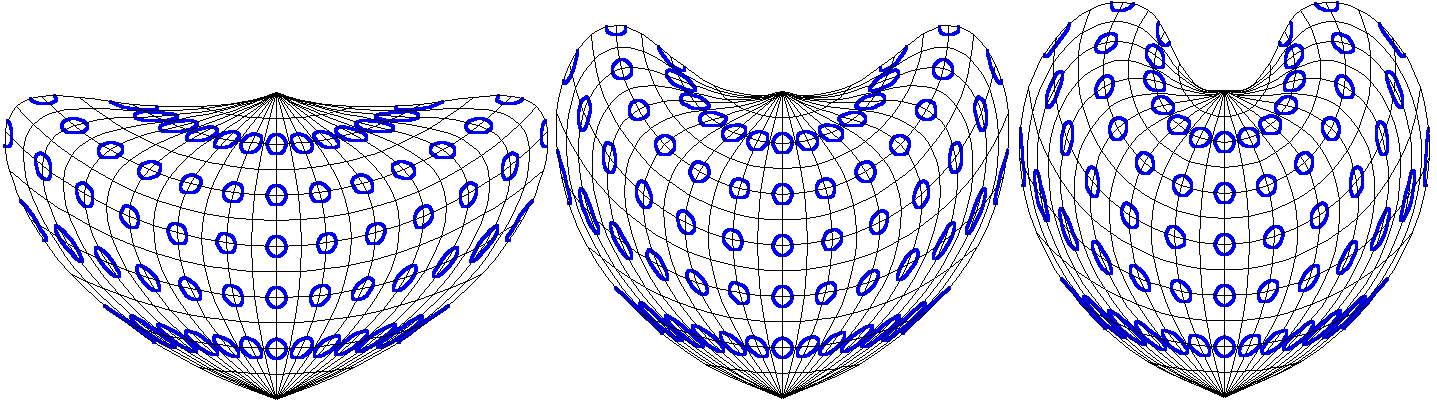
One possible alternative approach to an intermediate position between the Sinusoidal and Werner projections would be to adopt the approach of constructing conical projections from circular projections, and to apply this to the Werner projection. In this case, this would result in a projection drawn with lines of latitude as equally spaced concentric circular arcs centred on the pole, with arc lengths equal to a given fraction of their lengths on the globe, and placed symmetrically across the vertical central meridian. This would also be an equal area projection, and in the limit would produce the Werner projection when the fraction approached one; but for small values of the fraction all areas of the map would seem excessively narrow east-west, and in the limit the map would disappear as the fraction approached zero. Stretching the map along the horizontal axis can rectify these two flaws, and the approach suggested below does so by an amount equal to the inverse of the fraction. The effect is to turn the circular arcs of latitude into arcs of similar ellipses (i.e. with constant eccentricity), and to ensure that in the limit this would produce the Sinusoidal projection when the fraction approached zero. Since each transformation preserves area, the resulting projection is still an equal area projection.

The suggested alternative projection therefore draws lines of latitude as constant eccentricity concentric elliptical arcs centred on the pole, and placed symmetrically and equally spaced across the vertical central meridian. The elliptical arcs are determined by drawing circular arcs centred on the pole, with arc lengths equal to a given fraction of their lengths on the globe, and then stretching these arcs horizontally by the inverse of the fraction. Changes to this fraction vary the details of the projection. In the limit, this produces a Werner projection when the fraction is one, and a Sinusoidal projection when the fraction approaches zero.

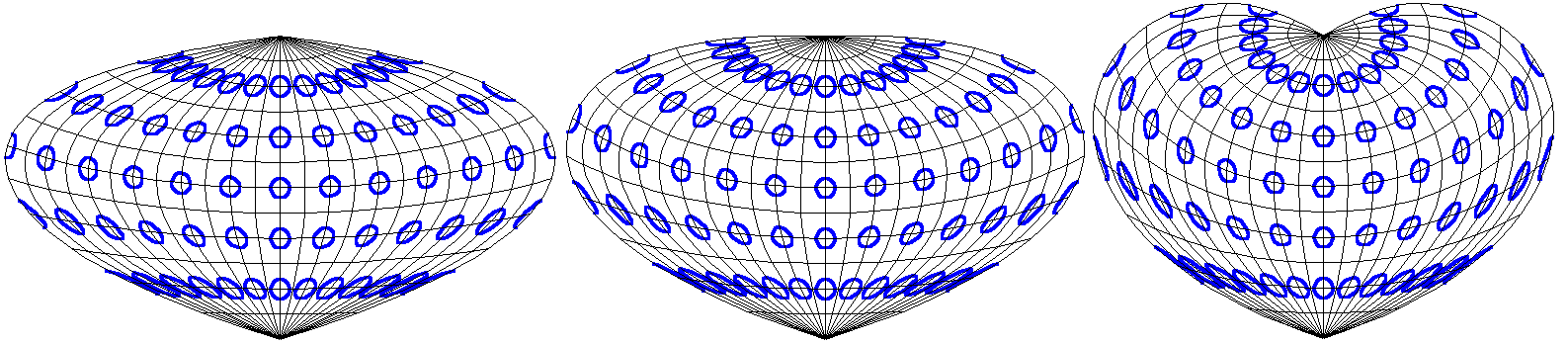
One of the advantages of the suggested alternative over the Bonne projection is that it appears as a less complex shape for the world as a whole, especially when the fraction chosen is ¹/₂, in which case the two representations of the antipodal meridian are horizontal near the North Pole. It does not repeat the Bonne projection’s possibility of a meridian going (from South to North) up, then down, and finally up again. Like the Sinusoidal, Werner and Bonne projections, it is equal area throughout and has low distortion close to the central meridian. Since all four projections are equal area, they cannot be conformal, and so must distort shapes in parts of the map. Like the Bonne projection, the alternative can be varied, and this will affect the shape distortion in different locations. The Sinusoidal and Bonne projections have low shape distortion along on a line of latitude: the Sinusoidal on the equator and the Bonne on its standard parallel; the Werner has low shape distortion near the North Pole. However the shape distortions can become much greater at other points, especially near the antipodal meridian. The alternative projection does not share this property: everywhere away from the central meridian has some shape distortion, so it has no standard parallel. Despite this, a greater area of the alternative has only moderate distortion.

If for example moderate distortion at a point is taken as stretching small parts of meridians near that point by a factor less than 2, then for the Sinusoidal projection only between about 33° S and 33° N do all points on the antipodal meridian have moderate distortion; for the Werner only north of about 8° N; and for the Bonne with a standard parallel at 30° N only between about 8° S and 67° N. For the alternative projection with a fraction of ¹/₂, all small parts of meridians north of about 30° S are stretched by a factor less than 2, even though no part of the antipodal meridian is stretched by less than 1.5. This more moderate impact on distortions at the sides of the map can make the alternative projection seem to be more visually attractive.

Formulae

A projection can only be used with defined formulae. The direct formulae enable the projections to be drawn using vector data, as with the meridians and parallels shown earlier, while inverse formulae enable the projections to be drawn using raster data as shown below.

The following equations are based on a sphere with radius 1; so angles are measured in radians and p (3.14159…) is the angle of two right angles.

l is the longitude (0 at the central meridian and ⁺/-p at the antipodal meridian) and j is the latitude (0 at the equator and ⁺/-^p/₂ at the poles).

X and Y are the co-ordinates on the resulting projection.

r and h are intermediate values used to simplify some of the calculations and illustrate the common pattern of the different projections.

y is used to help determine the precise variant of the Bonne or alternative projection.

The projections of points on the central meridian (i.e. with l =0) do not vary between the four projections, since the formulae then give X=0 and Y=j . In particular, the poles are projected to (0,^p/₂) and (0,^-p/₂). This makes comparisons of the resulting projections easy.

For the Bonne projection, y is the line of latitude with points with no shape distortion (the standard parallel) and cot(y ) is the radius of the circular arc which represents this line of latitude. y has no such simple meaning for the alternative projection, since all points away from the central meridian have shape distortion; it is used in the form sin(y ) to denote the fraction used which varies between 0 and 1 as y varies between 0 and ^p/₂.

For the Bonne and the alternative projection formulae, if y =^p/₂ then cot(y )=0 and sin(y )=1 respectively, and so the Werner projection formulae result immediately. If y =0 then neither cot(y ) nor 1/sin(y ) are finite; but it is not difficult to show that as y tends to 0, the limit of both is the Sinusoidal projection.

In the alternative projection, the eccentricity of the elliptical arcs of latitude is cos(y ). The fraction sin(y ) is ¹/₂ when y =^p/₆ in which case the eccentricity is Ö (³/₄) or about 0.866…, with the ellipses twice as wide as they are high.

Notes and references

Names of map projection are confusing, and some reflect their promoters more than their inventors or their properties. The Sinusoidal projection is sometimes known as the Sanson-Flamsteed or the Mercator Equal-Area projection; the Werner projection is sometimes known as the Stabius-Werner or the Stab-Werner projection; and the Bonne projection is sometimes known as the dépôt de la guerre or the Sylvanus projection.

The Sinusoidal and Bonne formulae given here were adapted from those that can be found from links at:

The projected graticules with examples of Tissot’s Indicatrix were drawn using Excel. Tissot’s Indicatrix involves taking circles of small but equal radius on different parts of the globe and showing how they are projected. The distortion can easily be seen when they are stretched in particular directions, although for equal-area projections as shown here, the areas of each resulting shape remains the same.

The maps adjacent to the formulae were adapted from those that can be generated at: