 |
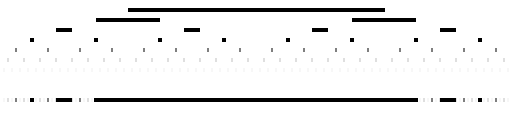
Illustrating the removal of intervals when k=1 |
This article provides a way of constructing nowhere dense sets with positive measure. From these it provides a strictly monotonic continuous function which has a dense set of points where the function has derivative of zero.
Consider the interval [0,1]. Remove from it each point which represents a dyadic fraction (one of the form a/2m in lowest terms, i.e. whose binary expression terminates, in this case with a and m positive, a odd and a<2m) and an interval around it. The remaining set of points (if any remain) is nowhere dense, and if the intervals are chosen suitably then the measure of the remaining points will be between 0 and 1. In this case the intervals removed will be of the form
[a/2m - k/22m, a/2m + k/22m]
with k real and 0<k<2. Taking k=0 would shrink each interval to a point, so removing a set of measure 0 and leaving a dense set of measure 1, while taking k=2 would remove all the points when the interval around 1/2 is removed leaving the empty set with measure 0.
The diagram below looks at the position when k=1. We start by removing [1/4,3/4]. Then we remove [3/16,5/16] and [11/16,13/16], though these overlap the interval already removed. Then we remove [7/64,9/64], [23/64,25/64], [39/64,41/64], and [55/64,57/64], though two of these were already removed in the first step. And so we go on, though the intervals removed quickly become so narrow that they cannot easily be seen; despite this the remaing set is nowhere dense since near any point an interval has been removed.
 |
Illustrating the removal of intervals when k=1 |
The numbers removed from [0,1] are those whose binary representation has the same digit from binary place m+1 to binary place 2m for some m>0, which differs from the digit in the mth binary place. (If they do not differ, then it may be worth considering a lower value of m.) The first step removes numbers of the form 0.01... and 0.10...; the second removes those of the form 0.0011..., 0.0100..., 0.1011..., and 0.1100..., though those of the form 0.0100... or 0.1011... will have already gone in the first step. Those which remain after all steps are those which do not have that property for any m. So for example, 1/3 written in binary starts as 0.0101010101..., and recurrs in the same pattern, so remaining in the nowhere dense set.
If there were no overlaps, the total measure of the intervals removed would be 1, but as there are overlaps, the measure removed is less than 1, leaving a set of positive measure which turns out to be 0.2677868402178891123766714...
The next diagram below looks at the position when k=1/2. We start by removing [3/8,5/8]. Then we remove [7/32,9/32] and [23/32,25/32]. Then we remove [15/128,17/128], [47/128,49/128], [79/128,111/128], and [111/128,113/128], though two of these overlap with the interval removed in the first step. And so we go on, though the intervals removed become smaller even more quickly.
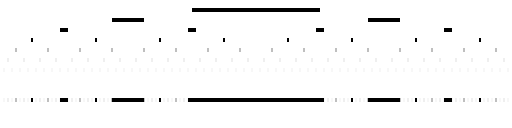 |
Illustrating the removal of intervals when k=1/2 |
If there were no overlaps, the total measure of the intervals removed would be 1/2, but as there are overlaps, the measure removed is less, leaving a set of positive measure of more than 1/2 which turns out to be 0.5355736804357782247533428..., exactly twice the result when k=1.
The relationship between the measure of the two remainging sets is not quite a coincidence, since the the measure of the interval remaining after given number of steps when k=1 is exactly half that after one fewer step when k=1/2. This suggests that it may be worth investigating f(k), the measuse of the nowhere dense set as k changes.
I cannot see any more nice observations, but the behaviour of k turns up some other interesting points. The chart below comes from calculating f(k) to a sufficient precision for a large number of values of k.
|
Illustrating how the measure f(k) of the nowhere dense set varies with k. |
There seem to be some easy observations:
There also seem to be some less easy observations:
Henry Bottomley. May 2005.