Consider the following set of problems for a polyhedron:
1a. "What is the shortest possible closed route on the surface of the polyhedron which crosses each face once?"
1b. "What is the shortest possible closed route on the surface of the polyhedron which visits each face?"
2a. "What is the shortest possible closed route on the surface of the polyhedron which crosses each edge once?"
2b. "What is the shortest possible closed route on the surface of the polyhedron which visits each edge?"
A closed route is one which has no starting or finishing point; it could be considered as one which finishes at its starting point - this could include a route which went from one point to another and then reversed the path returning to the first point. Crossing once excludes routes which just touch a face or edge, which run along part or all of an edge, or which cross more than once; visiting is a broader concept which might instead involve just touching, running along an edge, or crossing more than once.
Given the conditions for 1a and 2a (crossing once), there may not be a solution for a given polyhedron, either because the topology precludes any solution, or because there are a set of solutions whose greatest lower bound is not the length of any solution; in the latter case, we will describe this greatest lower bound as a "limit solution"
For a unit cube, with six faces and twelve edges, my best results so far (and I would not be surprised if they were indeed the solutions) are:
| 1a. | sqrt(18)= 4.2426406... |
| 1b. | sqrt(18)= 4.2426406... |
| 2a. | 6 (as a limit solution) |
| 2b. | sqrt(32)= 5.6568542... |
For a unit tetrahedron, with four faces and six edges, my best results so far (and again I would not be surprised if they were indeed the solutions) are:
| 1a. | 2 |
| 1b. | sqrt(3)= 1.7320508... |
| 2a. | topologically impossible |
| 2b. | sqrt(27/4)= 2.5980762... |
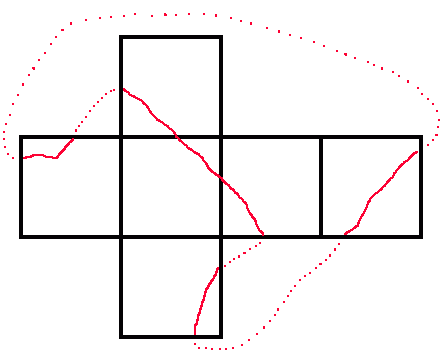
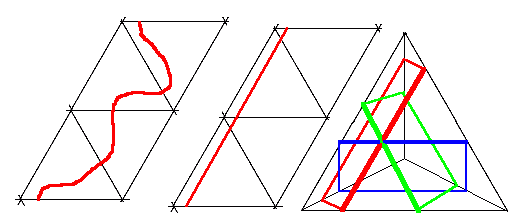
We are looking for a closed route which crosses each of the six faces. Clearly this involves entering and then leaving each face once each. We cannot leave each face by the same edge we enter (otherwise the adjacent face sharing the edge is crossed twice). Nor can we go directly across two consecutive faces (where directly across means entering a face across one edge and leaving across the parallel edge) as this would involve four faces wrapped around the cube, and would then require the route to pass from one of the remaining two faces to the other, which it couldn't as they are not adjacent. This then leaves essentially two possible topological routes (modulo various symmetries), one where the route does not go directly across any face, and one where it goes across two. They are:

But each of these nets can be redrawn so that the route stays inside the net, and since the route can in these cases be a straight line, then one of these straight lines would provide the shortest surface routes.
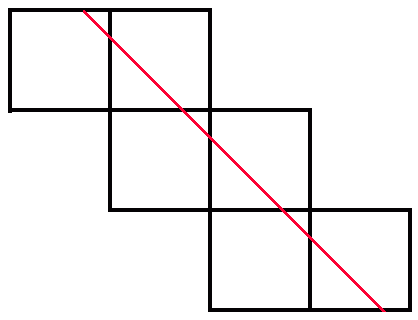
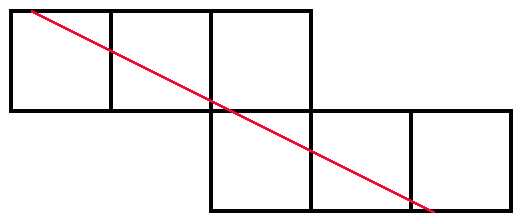
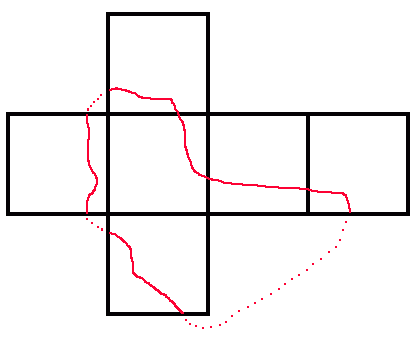
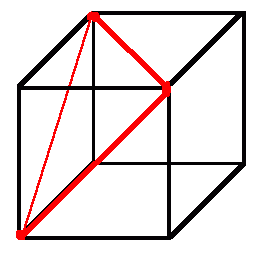
One has length sqrt(18) while the other has length sqrt(20) and so it is the former straight line (without the route going directly across any face) which provides the shortest possible closed route on the surface of a unit cube which crosses each face once. Indeed for any point not on the diagonal of a square face, there are two such shortest routes going through that point (parallel to the diagonals of the face) and for points on a diagonal (but neither at the centre of the face nor the corners) there is one (parallel to the other diagonal). As an example, the two routes here are minimal (they cross on the top and front faces and are the two shortest routes going through either of these points):
In my view this amounts to a proof.
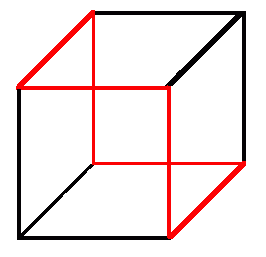
I cannot see a better route (there are several new routes which have the same length as before) and so my answer is the same: sqrt(18). One of those which is the same length uses a sort of greedy algorithm: at a single corner three faces can be visited without traveling any significant distance; for the next step obvious choices include another face at a distance 1, or two faces together at a distance sqrt(2) - we will choose the second as it provides more faces per unit of distance; so we now have an open route which visits five faces just by using a diagonal of a single face; the best way to visit the remaining face and close the route is to use two more diagonals of faces for a total distance of 3*sqrt(2)=sqrt(18).
It is conceivable that there might be a better route, but I would be surprised.
We can redraw the edges of the cube and its dual on a topological basis to discover the possible number of closed routes crossing each edge.
There is no point having a closed route which crosses itself on a face as replacing it by a closed route which cuts across two opposite corners of the face with straight lines (while remaining a single closed route) will not lengthen it (and will usually be shorter).
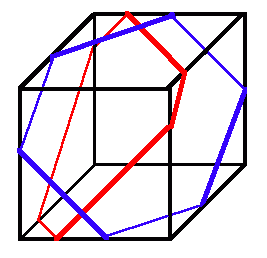
Clearly an open part (i.e. with two free ends) of a satisfactory closed route can cross three edges in a very small distance by looping round a corner. But to cross four or five it will need to be of length at least 1. To cross six or seven it will need to be of length at least 2; the possibility of an open route looping round the opposite corners of a single face could provide six edge crossings with a length less than 2, but this could not form part of a satisfactory closed route because all four edges of that face would have been crossed (as well as two other edges) and so the complete closed route could not then cross the other six edges of the cube. Similarly the open part of a satisfactory closed route crossing eight or nine edges would need to be of length at least 3, crossing ten or eleven edges at least 4, and crossing all twelve edges at least 5. The closed route crossing all twelve edges would therefore need to be at least 6. This provides a lower bound of 6 for the result.
But there is a satisfactory solution which can be as close to 6 as is desired. It involves starting at the midpoint of an edge, crossing a second edge close to one of the corners at the end of the first edge, going to the midpoint of the third edge meeting at that corner and then repeating the process five more times so as to cross all of the other edges before returning to the starting point. By using straight lines and moving the crossing points close to corners even closer, 6 is approached (the limit is when the route converges on edges of the cube). So 6 is a limit solution.
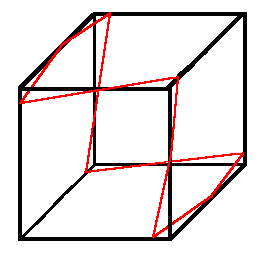
With some tightening of the outline of why 6 is a lower bound, I believe this would be a proof.
The previous case had a lower bound which depended on each edged being crossed once. Without this requirement, it would be possible to visit each edge with a shorter closed route. For example, it is possible to have a route which visited three new edges at four corners. Clearly in this case no pair of corners could be the ends of a single edge and so the closed route would amount to four diagonals of faces with a length of 4*sqrt(2) or sqrt(32).
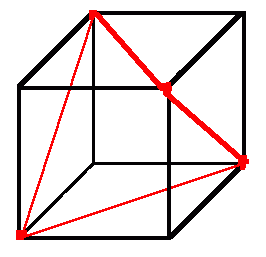
This obviously is not a proof, but it seems unlikely that there is a shorter closed route visiting all twelve edges.
We are looking for a closed route which crosses each of the four faces. Clearly this involves entering and then leaving each face once each. We cannot leave each face by the same edge we enter (otherwise the adjacent face sharing the edge is crossed twice). This leaves essentially only one possible topological closed route (modulo various symmetries). The straight line route will be the shortest and is of length 2. As far as I am concerned, this is a valid proof.
On each face the shortest closed route is parallel to one of two non-intersecting edges of the tetrahedron. Though any point not on an edge, there are three shortest closed routes (parallel to the three edges of the face it is on); while though a point on an edge (though not a corner) there are two.
Again we can reach a potential solution using a greedy algorithm: at a single corner three faces can be visited without traveling any significant distance; the nearest point of the remaining unvisited face is a distance sqrt(3)/2 away, so a closed route which visits it and returns will have a length sqrt(3). Again it is conceivable that there might be a better route, but I would be surprised.
It is not necessary to visit a corner to have a route of this distance. Instead we could start anywhere on an edge apart from its ends or midpoint (two faces visited), move away perpendicularly from this original edge to another edge (third face visited) and then continue across the third face so that we meet the fourth face perpendicularly on the edge between the third and fourth faces. So far this open route visiting four faces (though only crossing two faces) also has a length sqrt(3)/2 so to close the route we return by the same route for a total distance again of sqrt(3). Each point on the tetrahedron has at least three such routes passing through it (those on edges but on corners have four).
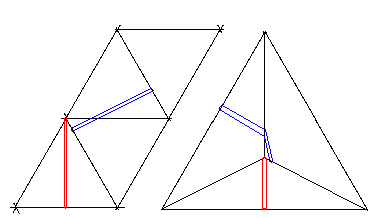
This is clearly not a proof, but the lengths involved are short enough to make it plausible.
There is no such route as each triangular face of a tetrahedron has three edges (an odd number) while a closed route requires each face to have an even number (so that the number of times the closed route enters and exits each face are equal). This is one of the simplest applications of Euler's work which started with the Königsberg bridges.
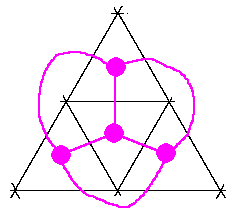
The same impossibility will occur with any polyhedron which has any face with an odd number of edges, including the other regular polyhedra apart from the cube (an octahedron and an icosahedron with triangles, and a dodecahedron with pentagons).
A greedy algorithm would suggest a solution which is not in fact the shortest, thus raising questions about its earlier use. The three sides of a single face would provide a closed route visiting each edge of the tetrahedron for a length of 3. Alternatively, we could start at a corner (three edges and no significant distance), connect to a second corner (visiting the fourth and fifth edges for a distance of 1). The shortest route to the sixth edge and then completing the route would involve a further distance of sqrt(3) by using two triangle altitudes for a total distance of 1+sqrt(3)=2.732... As far as I can see there is no net for which this is a straight line.
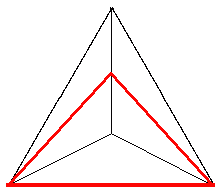
But we can easily do better than this, since unfolding to a net does not produce a straight line. If we start at a corner (three edges) then the shortest route which visits the remaining three edges on the opposite face and returns to the starting point has length sqrt(7)= 2.645... This can be seen as a straight line on a net which involves a reflection. But even this is not the best solution.
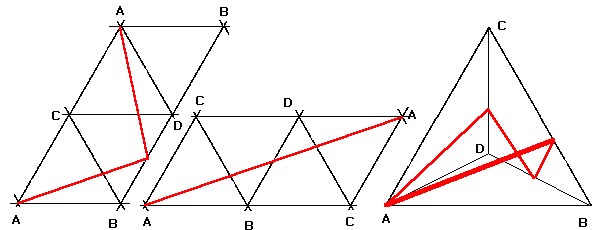
We can do even better with the following route: take the midpoints of the edges of one of the faces. Join each midpoint to the other two edges of the other triangular faces they are, on with lines which are perpendicular to these other edges. These six lines form a closed route which touches three edges and which crosses the other three with a total length of 6*sqrt(3)/4=sqrt(27/4)=2.598... There is also a sense in which this is a straight line on a net that involves reflections as well as unfolding, which inspires a little bit of confidence. Using this particular net and topological route, it is not difficult to show that starting and finishing at the mid-point of an edge produces the shortest distance, and so it is shorter than the previous example (which is a straight line on the same net but starting and finishing at a corner). This is my solution.
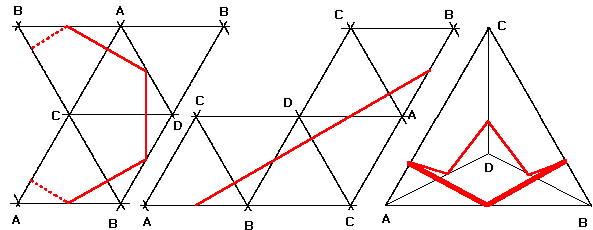
We now know that a closed route through a corner is not the shortest possibility. But starting from somehere else on an edge only provides a number of reasonable possible straight routes on a net (including reflections) which meet six edges (one which meets more than six will usually be longer and certainly will not be shorter): the picture below shows those for a closed route starting and finishing on the midpoint of an edge. For some of these, the mid-point will not be the shortest possibility (moving the starting and finishing point towards a corner can in some cases meet the requirements of the question while reducing the length towards sqrt(7) or sqrt(27/4) when it starts from a higher figure). But only the net in the example immediately above and its equivalents allow the possibility of going lower than sqrt(7) and is minimised as in that example with a length of sqrt(27/4). Putting this together is close to a proof that sqrt(27/4) is indeed the best solution.
Henry Bottomley, September 2001
Jim
Ferry has written in usenet:
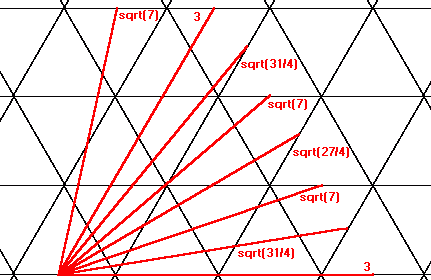
"The minimal circumnavigation is sqrt(3)*E/4, where E is the
number of edges. Referring to the graph [immediately above]
let a, b, and c be the number of crossings of each family of
parallel lines. The total length of the corresponding path is
sqrt((a^2 + b^2 + c^2) / 2), and a, b, and c must satisfy: a + b
+ c = 0, and |a|+|b|+|c|=E. Let a be the largest in absolute
value. Then |a|=|b|+|c|=E/2. The distance is minimized for |b|=|c|=E/4,
which is allowed provided E is even. This yields sqrt(3)*E/4. The
minimum is achieved if the edge graph has a Hamiltonian. "
He suggested that this might also extend to an octahedron (12 edges) and an icosahedron (30 edges). I have found that such an extension does not work, since there are shorter closed surface routes visiting each edge. This may be because (unlike the tetrahedron) the shortest routes could involve going through corners.
My shortest closed surface routes visiting each edge (question 2b) for regular polyhedra with unit edges are so far:
| Tetrahedron | 6 edges | sqrt(27/4) | 2.598... |
| Cube | 12 edges | sqrt(32) | 5.656... |
| Octahedron | 12 edges | 4 | 4.000 |
| Dodecahedron | 30 edges | 6+sqrt(180) | 19.416... |
| Icosahedron | 30 edges | sqrt(108) | 10.392... |
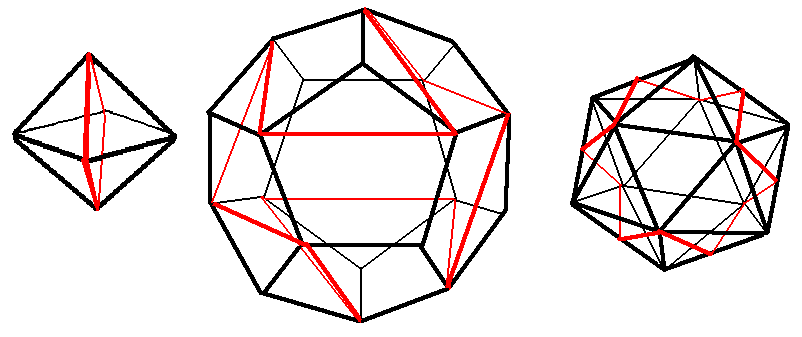
For the unit octahedron, the route shown is four edges; it is extremely efficient, and so is very likely to be the shortest possible solution. For the unit dodecahedron, the route shown is made up of a diagonal of each face (so is 12 times the golden ratio); while for the unit icosahedron, the route shown is made up of 12 altitudes of triangles. These last two may or may not be the shortest: let me know if you can find any shorter surface closed routes which visit every edge. All three of the routes shown here (unlike the cube or the tetrahedron) are symmetric in terms of reflection through the centre of the polyhedron.
Jim Ferry also suggested that I include the surface Steiner trees here, i.e. the shortest trees on the surface which join every corner. This doesn't quite fit the pattern of "shortest closed route" used in the other questions on this page, but it would certainly be more interesting than the shortest closed route visiting each corner, which is simply the number of corners, since each of the Platonic solids has a Hamilitonian circuit on its edges. But see below as to why considering Hamiltonian circuits are not a complete waste of time.
He calculated that the lengths of the Steiner trees are sqrt(7)=2.645... for a tetrahedron and 3+sqrt(12)=6.464... I agree, though I am mildly surprised by the tree for cube, which is the trees for two squares joined by an edge. The tree for a tetrahedron is simply a folded tree for the rhombus made up of two equilateral triangles.
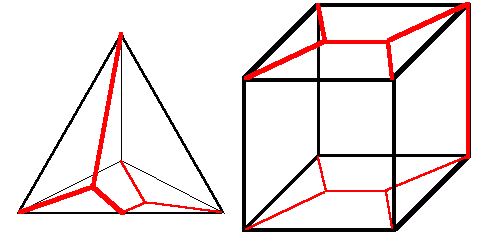
Jim Ferry also thought that the minimal Steiner trees for the octahedron and icosahedron have lengths sqrt(7)+sqrt(3) and sqrt(7)+4*sqrt(3). These are formed by augmenting the rhombus solution with (V-4)/2 triangle solutions. The intuition behind the minimality is that assuming the initial hit of sqrt(7) is unavoidable, adding an additional sqrt(3)/2 per vertex is optimal (assuming the planar result holds for these surfaces - and he doesn't see why it shouldn't). He pointed out Steven Finch's page on Steiner trees.
We could also consider the other questions for these other regular polyhedra: we already know that there are no solutions to question 2a for any of them apart from the cube. For question 1a, we could start by looking at Hamiltonian circuits on edges visiting every corner. In themselves, they not of great interest because their length is equal to the number of corners of a regular polyhedron (so the results would be 4 for a unit tetrahedron, 8 for a cube, 6 for an octahedron, 20 for a dodecahedron and 12 for an icosahedron).
However knowledge of them helps provide solutions to question 1a, since a Hamiltonian circuit of a regular polyhedron is equivalent to a closed topological route crossing each face of the dual polyhedron once. So since (modulo symmetries) there is only one Hamiltonian circuit of a tetrahedron, one of a cube, two of an octahedron, one of a docahedron, and many of an icoashedron, this implies that there is (modulo symmetries) only one closed topological closed route crossing each face of a tetrahedron once, one for an octahedron, two for a cube, one for an icosahedron, and many for a dodecahedron. The case of a cube and a tetrahedron are covered above. The diagram below shows these Hamilitonian circuits (though it only has one of the many examples for an icosahedron).
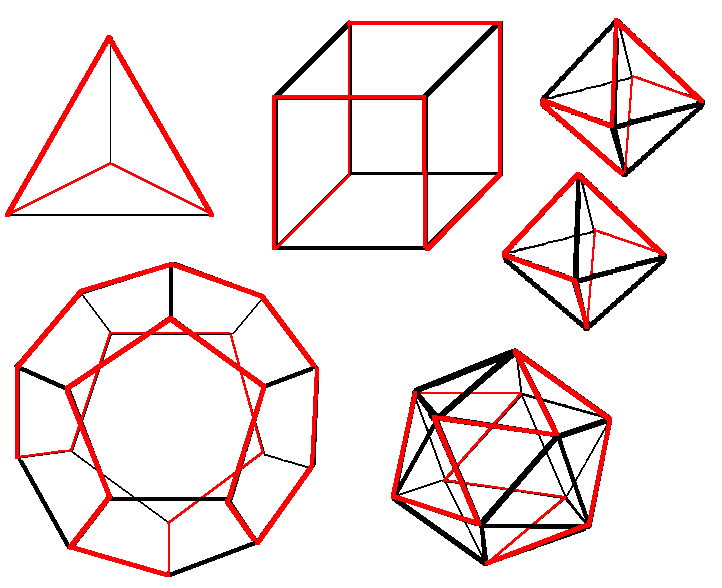
So for a unit octahedron, question 1a is quite easy as (like the tetrahedron) there is only one possible topological route, and so making this a straight line gives a shortest distance of sqrt(12)=3.464... It can be drawn by starting on any edge (apart from a corner or a midpoint) and moving away perpendicularly, continuing in a straight line (including across edges as if the octahedron had been unfolded) until we return to the starting point. I suspect that the answer to question 1b for a unit octagon might be the same.
For a unit icosahedron, question 1a is only slightly more complicated. There is not a straight line on the unfolded net which is equivalent to the single topological route, but it is possible to draw a succession of four straight lines which have a greatest lower bound of a length of 2+sqrt(28)=7.291... as a limit solution.
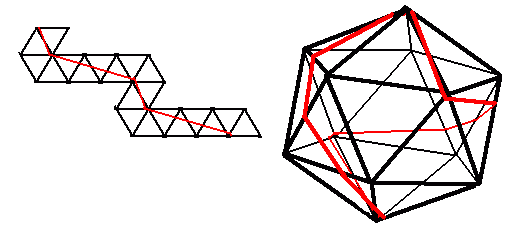
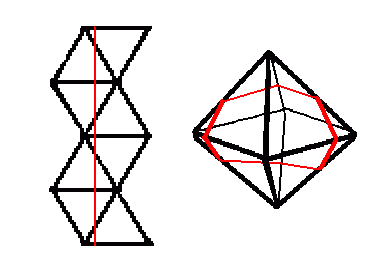
A unit dodecahedron is undoubtably more complicated and I would welcome any suggestions. To take just one possible Hamiltonian on an icosahedron (essentially the example illustrated among the Hamiltonians above which has some nice symmetries), we can then construct the equivalent topological route crossing each face of a dodecahedron once, and then find the corresponding limit solution for that route, as illustrated below. I think that the limit in this particular case is then 4*sqrt(4+sqrt(5))=9.988... but as yet I have no particular reason to believe that this is necessarily the solution of the dodecahedral version of question 1a (apart from the nice symmetries).
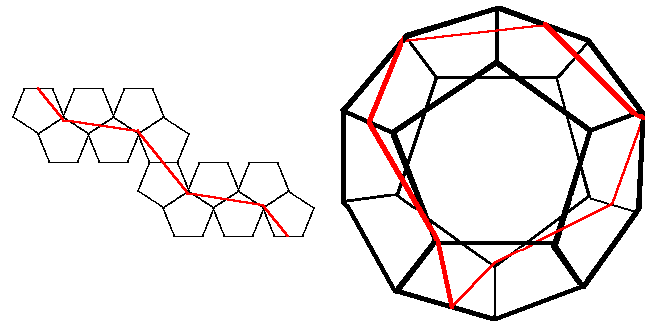
So my shortest closed surface routes crossing each face once (question 1a) for regular polyhedra with unit edges are (including the uncertain figure for the dodecahedron):
| Tetrahedron | 4 faces | 2 | 2.000 |
| Cube | 6 faces | sqrt(18) | 4.242... |
| Octahedron | 8 faces | sqrt(12) | 3.464... |
| Dodecahedron | 12 faces | sqrt(64+sqrt(1280)) (as a limit solution) | 9.988... |
| Icosahedron | 20 faces | 2+sqrt(28) (as a limit solution) | 7.291... |
The nature of Internet search engines is such that some people arrive at this page looking for rather more basic information than provided above. Here is some information designed to be useful to such visitors:
| Faces | Edges | Corners (or Vertices) |
Edges (and corners) on each face |
Edges (and faces) meeting at each corner |
|
| Tetrahedron | 4 | 6 | 4 | 3 | 3 |
| Cube | 6 | 12 | 8 | 4 | 3 |
| Octahedron | 8 | 12 | 6 | 3 | 4 |
| Dodecahedron | 12 | 30 | 20 | 5 | 3 |
| Icosahedron | 20 | 30 | 12 | 3 | 5 |
It becomes even clearer that the Cube and the Octahedra are duals, as are the Dodecahedron and the Icosahedron, while the Tetrahedron is its own dual. The next table shows the surface area and volume of each Platonic polyhedron with edges of length 1: remember that in each case areas are proportional to the square of the edge length while volumes are proportional to the cube of the edge length. Note that a unit Cube is larger than a unit Octahedron, and that a unit Dodecahedron is larger than a unit Icosahedron.
| Surface Area | Volume | |||
| Tetrahedron | sqrt(3) | 1.732... | sqrt(1/72) | 0.117... |
| Cube | 6 | 6.000 | 1 | 1.000 |
| Octahedron | sqrt(12) | 3.464... | sqrt(2/9) | 0.471... |
| Dodecahedron | sqrt(225+sqrt(40500)) | 20.645... | 15/4+sqrt(245/16) | 7.663... |
| Icosahedron | sqrt(75) | 8.660... | 15/12+sqrt(125/144) | 2.181... |
Henry Bottomley October 2001
Other pages: Henry Bottomley Surface distances on a cube or cuboid All rights reserved