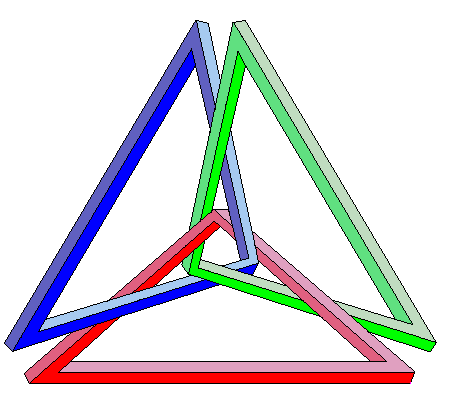
Here is a picture. What is odd about it?

Some suggestions:
The picture above is a combination of the two classic pictures below:
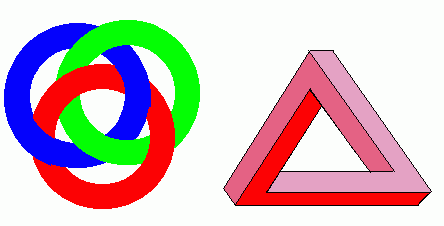
The first of these has three rings and is known as the Borromean Rings. Although they are interlinked as a triple, no pair of them is linked; remove one of them and the other two are not linked. They cannot actually be made as ordinary circular rings, though they can be made out of string or other shapes in three dimensions.
The second is designed to seem to be a three-dimensional triangle. Following the sides round (either clockwise or anti-clockwise) reveals the changing perpective and why this is known as the Impossible Triangle.
Do you think that the top picture works as an optical illusion? Or is it just too complex? Any comments would be welcome.
Here is another impossible picture using a similar structure:
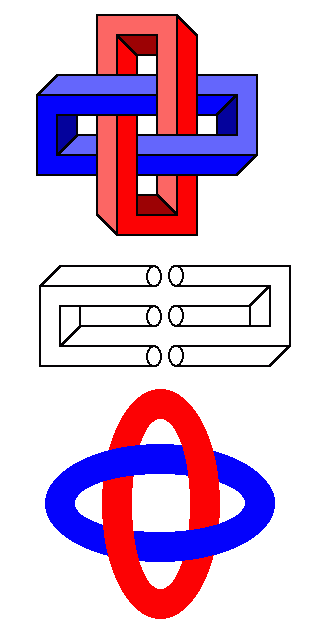
The top of these three pictures intertwines two impossible rectangles to make a mysterious cross.
The second pretends to show how to construct an impossible rectangle by combining the optical illusion of a cricket wicket with its own rotation.
The third shows the intertwining of two elliptical shapes (which would requiring some bending in three dimensions to be possible).
Returning to triangles, here are two knots: a left-handed trefoil knot and a right-haded trefoil knot. Does either look better than the other?

© Henry Bottomley October 2001and June 2002. How about looking at circumnavigating a cube and a tetrahedron? Or the 216, 212, 22 or 8 browsersafe colours for web pages? Or Pythagoras's theorem in moving pictures? Or seven formulae for the area of a triangle? Or Medians and area bisectors of triangles? Or Java World Map Projections (including a triangular equal area projection).