See also Henry Bottomley's Look and Say Java Script, Evolution of Conway's Elements and Seven Complete Orderings
Reproduced by Henry Bottomley with permission
© Copyright 1993 Mario Hilgemeier
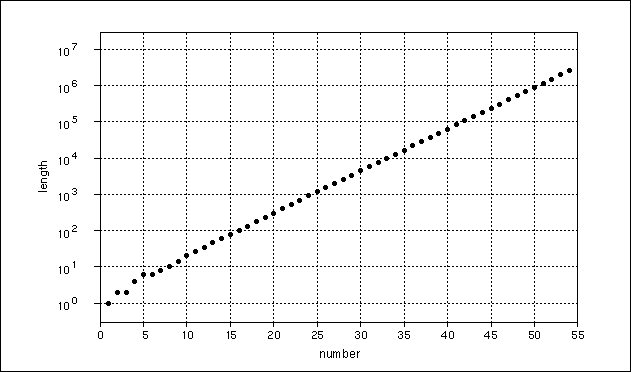
Consider these strings: 1, 11, 21, 1211, 111221, 312211, ... what is the next item? If you think its 13112221, you're right. Why? Speak aloud, "one" 1, "this is one one" 11, "now we have two ones" 21, "thats one two and one one" 1211 - you get the idea. Therefore Conway has called the iteration rule "audioactive". I've called it "Gleichniszahlenreihe" (GZR, see glossary), because of its analogy with meaning (what does 11 mean? 1 ), description (what is 11? 21), and growth because the string length (i.e. the number of characters) grows regularly (exponentially) with a factor of about 1. 303577269 (in the limit), according to Conway [13] (Figure 7.2).

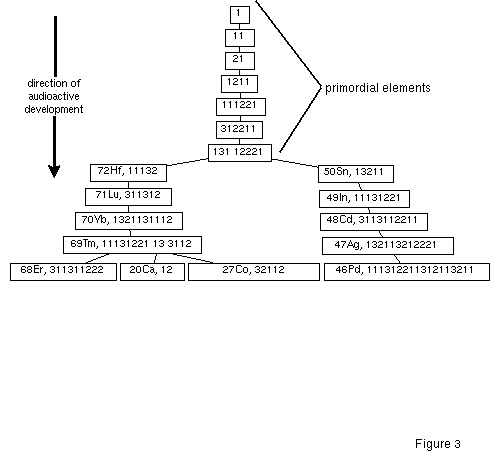
Conway was the first to discover that these strings, growing exponentially in length, do split "naturally" at certain points. After such a split, each of the fractions develops without influencing the other any more; then it splits again. Such a fraction is called an "element". An example of this split is shown in figure 3. The last string of the primordial elements, 13112221, splits into 131 and 12221; this is indicated by a space. In the following audiactive decay the pair 11 (where the split occurs) is changed to 21. But the resulting two parts 11132 and 13211 can be considered as independent in the next stages. For instance, the string called 71Lu in figure 3 develops from 72Hf; we do not need to know that the whole string is longer.
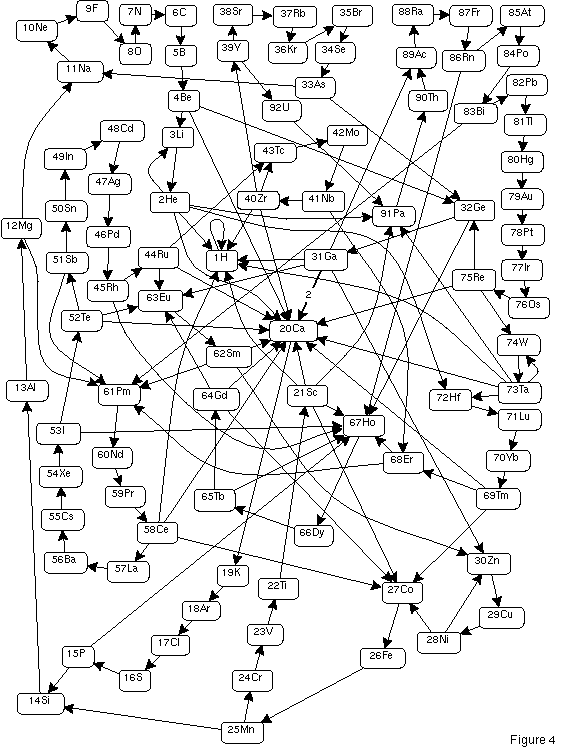
In analogy to the decay of radioactive elements, Conway called the splitting process "decay". If you start with the number 1 (or any other character) and let it grow for some hundred iterations, you get only 92 (mostly instable) elements of the audioactive decay. Because there are also 92 known (stable) chemical elements in nature, and some of them change by radioactive decay, Conway named them uranium (U), protactinium (Pa) down to helium (He) and hydrogen (H) . Each of these elements (except hydrogen) transmutes into another or splits into two or more elements. In this "nuclear-chemical" view, the Gleichniszahlenreihe starts with a "primordial element" 1, which rapidly develops into the elements Hafnium (Hf,11132) and Tin (Sn, 13211). A "primordial element" (see figure 3) is an element that never recurs in audioactive decay. Figure 4 shows the complete development scheme for all 92 elements.
In table 1 (a table of elements) you find a column denoted "element abundance". The abundance of an element is defined as the number of atoms of each element per million atoms. The appropriate measuring unit is "ppm", parts per million. How can we compute the abundance of an element - why do they have particular abundances anyhow? We will consider this question below.
Element abundance in ppm length string 92 U 102.56285249 1 3 91 Pa 9883.5986391 2 13 90 Th 7581.9047124 4 1113 89 Ac 6926.9352045 4 3113 88 Ra 5313.7894999 6 132113 87 Fr 4076.3134078 10 1113122113 86 Rn 3127.0209328 12 311311222113 85 At 2398.7998311 7 1322113 84 Po 1840.1669683 10 1113222113 83 Bi 1411.6286100 10 3113322113 82 Pb 1082.8883286 9 123222113 81 Tl 830.70513293 12 111213322113 80 Hg 637.25039755 14 31121123222113 79 Au 488.84742983 18 132112211213322113 78 Pt 375.00456739 24 111312212221121123222113 77 Ir 287.67344775 28 3113112211322112211213322113 76 Os 220.68001229 34 1321132122211322212221121123222113 75 Re 169.28801808 42 111312211312113221133211322112211213322113 74 W 315.56655252 27 312211322212221121123222113 73 Ta 242.07736666 32 13112221133211322112211213322113 72 Hf 2669.0970363 5 11132 71 Lu 2047.5173200 6 311312 70 Yb 1570.6911808 10 1321131112 69 Tm 1204.9083841 14 11131221133112 68 Er 1098.5955997 9 311311222 67 Ho 47987.529438 7 1321132 66 Dy 36812.186418 12 111312211312 65 Tb 28239.358949 16 3113112221131112 64 Gd 21662.972821 11 13221133112 63 Eu 20085.668709 7 1113222 62 Sm 15408.115182 6 311332 61 Pm 29820.456167 3 132 60 Nd 22875.863883 6 111312 59 Pr 17548.529287 8 31131112 58 Ce 13461.825166 10 1321133112 57 La 10326.833312 5 11131 56 Ba 7921.9188284 6 311311 55 Cs 6077.0611889 8 13211321 54 Xe 4661.8342719 14 11131221131211 53 I 3576.1856107 18 311311222113111221 52 Te 2743.3629717 13 1322113312211 51 Sb 2104.4881933 7 3112221 50 Sn 1614.3946687 5 13211 49 In 1238.4341972 8 11131221 48 Cd 950.02745645 10 3113112211 47 Ag 728.78492056 12 132113212221 46 Pd 559.06537945 18 111312211312113211 45 Rh 428.87015042 24 311311222113111221131221 44 Ru 328.99480576 21 132211331222113112211 43 Tc 386.07704943 15 311322113212221 42 Mo 296.16736852 20 13211322211312113211 41 Nb 227.19586752 29 11131221133221131112211312221 40 Zr 174.28645997 23 12322211331222113112211 39 Y 133.69860315 7 1112133 38 Sr 102.56285249 7 3112112 37 Rb 78.678000089 10 1321122112 36 Kr 60.355455682 14 11131221222112 35 Br 46.299868152 16 3113112211322112 34 Se 35.517547944 20 13211321222113222112 33 As 27.246216076 26 11131221131211322113322112 32 Ge 1887.4372276 23 31131122211311122113222 31 Ga 1447.8905642 17 13221133122211332 30 Zn 23571.391336 3 312 29 Cu 18082.082203 6 131112 28 Ni 13871.124200 8 11133112 27 Co 45645.877256 5 32112 26 Fe 35015.858546 8 13122112 25 Mn 26861.360180 12 111311222112 24 Cr 20605.882611 5 31132 23 V 15807.181592 8 13211312 22 Ti 12126.002783 14 11131221131112 21 Sc 9302.0974443 16 3113112221133112 20 Ca 56072.543129 2 12 19 K 43014.360913 4 1112 18 Ar 32997.170122 4 3112 17 Cl 25312.784217 6 132112 16 S 19417.939250 10 1113122112 15 P 14895.886658 12 311311222112 14 Si 32032.812960 7 1322112 13 Al 24573.006695 10 1113222112 12 Mg 18850.441227 10 3113322112 11 Na 14481.448773 9 123222112 10 Ne 11109.006821 12 111213322112 9 F 8521.9396539 14 31121123222112 8 O 6537.3490750 18 132112211213322112 7 N 5014.9302464 24 111312212221121123222112 6 C 3847.0525419 28 3113112211322112211213322112 5 B 2951.1503716 34 1321132122211322212221121123222112 4 Be 2263.8860324 42 111312211312113221133211322112211213322112 3 Li 4220.0665982 27 312211322212221121123222112 2 He 3237.2968587 32 13112221133211322112211213322112 1 H 91790.383216 2 22
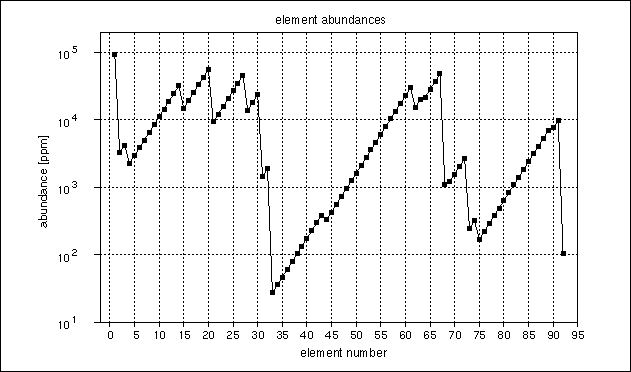
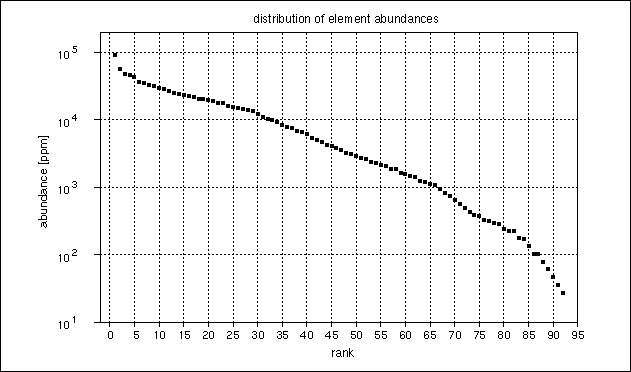
The sawtooth-like form of the element abundances when drawn as a function of element number (figure 5) is caused by the decay process. There are certain development chains in which one element decays into exactly one other element. One instance of such a loop is the chain starting at 61Pm (middle left in figure 4). Because generally the development is from higher to lower element numbers, and because the total string length grows with each decay step, the higher element numbers in a decay chain are "better fed". Because of the many decay chains the sawtooths in figure 5 occur. You can see this also in table 1: abundances of elements with only one successor are exactly 1.303577269 (the growth factor) times greater than their successor (e.g. 60Nd and 59Pr). When the abundances of the elements are ordered by rank (starting with the highest abundance) nothing special can be seen (figure 6).
A context-sensitive string-rewriting system can be defined in this way: Every character of the previous string is transformed according to its context (its neighboring ciphers or characters). This is exemplified in the GZR by the fact that a 1 doesn't always develop in the same way, depending on the ciphers that are before and after it in the string. In contrast, in a context-free grammar each character develops in a certain way, independent of its neighbors (See exemplary L-system below). By defining his elements, Conway achieves something remarkable: a context-sensitive grammar can be seen as a context-free grammar by going to the higher level of the "elements". Both grammar types are present in the same iterated system. At the start, when primordial elements develop, everything is context-sensitive. But as soon as the first elements appear, the context-free view becomes possible.
Is the ordering of the elements in Table 1 really forced; that is, is it the only one possible? When you look at figure 4, you will find elements that have two or more outgoing arrows (e.g. 2He, 4Be, 31Ga, 32Ge). These elements develop into two or more elements. At these junctions one could change Conway's ordering. I would be interested to hear from readers who find an alternative ordering. This is the "labyrinthine" aspect of the GZR. [HB Note: there are seven such complete orderings - see Henry Bottomley's demonstration]
The generated strings 1, 11, 21, 1211 etc. can be interpreted as a number system with the base 3 (but without the zero). When position is counted from right to left, the first position has the multiplier 1(= 3^0), the second 3(= 3^1), the third 9(= 3^2), the forth 27(= 3^3) and so on. The number 10 in this system is written as 31(= 3*3 + 1*1), the decimal number 23 can be expressed as 212 (= 2*9 + 1*3 + 2*1). A numerical interpretation of the Gleichniszahlenreihe (GZR) can be found in table 2. Can you find any interesting number interpretations of the GZR-strings? Are there significant number-theoretic aspects?
string number factorized 1 1 1 11 4 2^2 21 7 7 1211 49 7^2 111221 376 2^3 * 47 312211 886 2 * 443 13112221 4777 17 * 281 ...
See also Henry Bottomley's Look and Say Java Script, Evolution of Conway's Elements and Seven Complete Orderings
Reproduced by Henry Bottomley with permission
© Copyright 1993, Mario Hilgemeier, email: contact
homepage
