See also Henry Bottomley's Look and Say Java Script, Evolution of Conway's Elements and Seven Complete Orderings
Reproduced by Henry Bottomley with permission
© Copyright 1997 Mario Hilgemeier
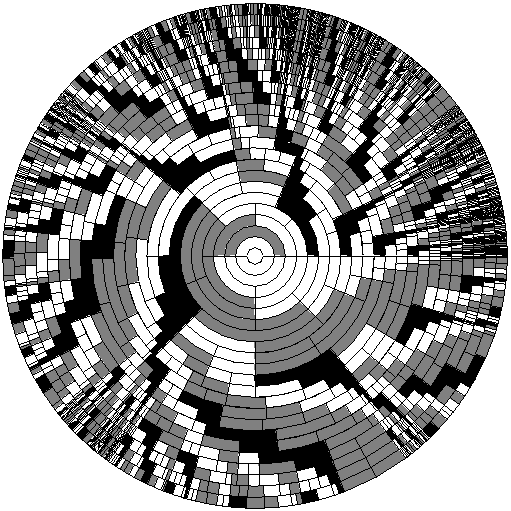
The image below is a representation of audioactive decay. The iteration started with "1" and was iterated 22 times.
The colour code is as follows: 1 = white, 2 = grey, 3 = black. The iterations are laid around the center ("1") in such a way that the description of an inner substring covers the same angle as that substring (note the thick grey radial spokes of "22"). Because of the black borders, strings of "33" are not clearly distinguished from a single "3"; but it can be inferred from the inner ring if it is a double "3" or not.
The horizontal border that extends to the right from the center corresponds to an angle of 0 degrees - there counting starts in counterclockwise direction. Note the repetition of start and end patterns of the iterates (period 3 of the beginnings and period 2 of the ends). Note also the colour field borders that go unbroken like spokes outward. These are separating lines for Conway's elements.
Because of the exponential growth of the string length, the colored fields soon become indistinguishable. It is interesting that certain regions exhibit faster growth than others which is seen in more densely spaced colour fields. This effect is a consequence of the fact that some elements multiply faster than others.
The first part grows faster than the last part which leads to a conterclockwise spiralling design. The self-similarity of the Gleichniszahlenreihe adds to this pleasing diagram which reminds me of certain Indian baskets.
I discovered the possibility of this representation in December 1996. After some pencil sketches I finally decided to write a perl program that produced the appropriate postscript code. For aesthetic reasons the diameter of the center was made smaller than twice the radius increase for the outer rings.

© Copyright 1993 Mario Hilgemeier
Now let's determine where the abundances come from. First, we
have to see that Conway's audioactive decay can be understood as
a
system of equations. The solution of this system of equations (by
iteration) gives the abundances.
Let me clarify this by a simpler string-rewriting system (like
the GZR). The GZR operates on ciphers, this example uses
characters.
There are five somewhat unusual characters to be iterated: "F",
"[",
"]", "+" "-". The iteration rule is:
"F" is expanded to
"F[+F][-F]". All other characters remain as they are.
Consider the pseudocode of the following system of equations.
It describes the growth of the number (abundance) for each of the
five characters from one development stage to the next. One
"F"
generates three new "F"s. The number of left brackets
"[" is the sum
of the number of extisting (old) left brackets plus those (new)
generated by the expansion of the "F" characters.
Fnew = 3 * Fold
[new = [old + 2*Fold
]new = ]old + 2*Fold
+new =+old + Fold
-new = -old + Fold
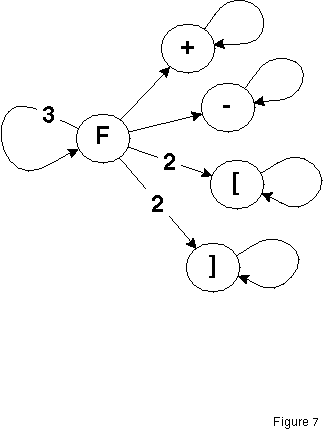
This system is visualized in figure 7 (in the style of figure 4). If you iterate this system, what will the abundances of the five characters be? If you don't see it at once, you could do the computation on a computer and see that the abundances of the characters eventually settle to 1/4 for F and each of the brackets, and 1/8 for the + and - characters. Of course, the growth factor is 3 because only F is responsible for the development of the system. This string rewriting system is one of the simpler L-systems [ 2, 3, 11]. When you experiment with pseudocode 1 (see appendix) you will generate fractal images of trees and bushes. Can you find similar interpretations for the strings of the GZR? Equation systems (almost always) have characteristic limit vectors and growth factors. This is exemplified by the above system and also by the GZR. The abundances of the GZR can be computed by pseudocode 2. Now you can see the relation of the exemplary L-system to the audioactive development. For instance, interpret pairs of ciphers of the GZR as drawing instructions. There are eight different pairs: 11, 12, 13, 21, 22, 23, 31 and 32 (33 never occurs, proof is given in [13]). Now interpret these eight pairs as letters of a graphical alphabet analogous to pseudocode 1, possibly with some extensions or redundancies. IÂve tried some simple interpretations, but they didnÂt show the (fractal) self-similarity which should be there because the iteration rule of the GZR is pure self-description. Can you find a beautiful interpretation of the GZR? L-systems are used in - Biology: modelling cell division patterns and morphogenesis research - Robotics: structural pattern recognition, speech recognition - Computer Science: semantics of programming languages [2] Beautiful pictures of plants can be found in the book by Lindenmayer and Prusinkiewicz[3]. The complex L-systems described there model the development patterns of plants, their growth and flowering patterns.
We see that a string can be the description of the state of a
system. If the system is a plant, then L-systems may be the
appropriate string rewriting systems (SRS) to model development
patterns. Other dynamical systems, in celestial mechanics for
instance, are described by a set of numbers (three dimensional
coordinates and impulses) and the equations governing the
relations
of the bodies (gravitation). The next set of numbers is derived
from
the previous by iteration because gravitational systems of more
than
two celestial bodies are not exactly solvable by symbolic
differential equations.
If a state is characterized by n numbers, it can be
represented as a point in n-dimensional space, the so-called
phase
space. As the system evolves, the point hops through phase space,
not always very smoothly (large jumps happen). Although the
description of the dynamical system by differential equations
yields
continuous movement, for reasons of computability the
representation
is transformed into a discrete dynamical system where iteration
is
used. But the introduction of iteration leads to discrete "jumps"
of
the system state (quantization).
Watching only one coordinate of the phase space is like
measuring any parameter (e.g. the rainfall per day) of a
dynamical
system (say, the weather). What you get is a time-series,
sometimes
a fractal curve (this depends on the type of dynamical system).
If
you enlarge portions of a fractal curve, they look "like the
whole
curve;" you find the same patterns after each renewed
magnification.
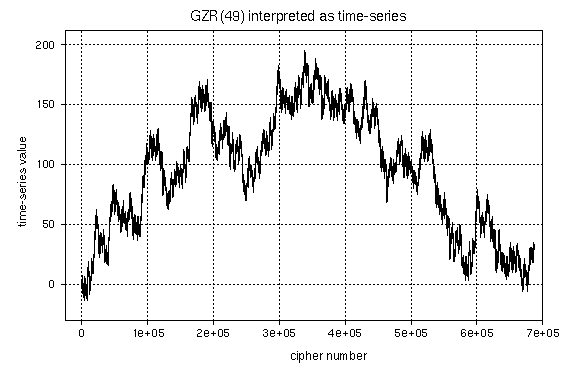
Any iteration of the GZR can be seen as a time-series. Figure
8 shows an example for the 49th iteration. How I arrived at this
curve is shown in pseudocode 3. This curve approaches
self-similarity because of the iteration rule of the GZR. But the
self- similarity is impure, because the line segments are finite.
When you examine the phase space for a given dynamical system, you find that certain regions will never be visited by the moving system state. In other regions however, the point density is very high - these are preferred states, visited often by the system. Phase spaces with two or three dimensions can be represented graphically very easily. Plot a point for each iteration of a nonlinear dynamical system. The geometrical shapes that evolve may be peculiarly beautiful or fractal [8, 9]. If the shapes are fractal, they are called strange attractors. Many readers may be familiar with the beautiful fractal images from the theory of dynamic systems[11, 14]. The length of time for which predictions are valid for nonlinear dynamical systems (weather, solar system) depends on our (limited) knowledge of the initial conditions. Because system states that are very close in phase space can get farther and farther apart in the future, our prediction ability is as limited as our knowledge of the initial conditions. Systems of orbiting bodies in celestial mechanics that have rational proportions of orbital periods become unstable sooner or later. Therefore it has been said that the stability of the solar system crucially depends on the irrationality of the proportions of the orbital periods. Well, for the foreseeable future, no disaster looms, as far as computer models go today. Computers often model states of the real world. By computation, limited prediction and explanation of the phenomena of the world becomes possible.
A robot must have an internal model of the world around it -
at least of those qualities of the environment that it needs for
its
function. For example, a washing machine is concerned with
laundry
type, water, temperature, detergent, time and the like. The model
of
the environment of the robot is represented in the tiny computer
by
a set of numbers and rules, hence we have met another kind of
phase
space here. The robotÁs state has a position in this
many-dimensional phase space. The robotÁs internal
representation of
its "position in the world" moves in phase space. If it
is to be a
successful robot, it will learn what the best actions are in
certain
regions of the phase space (e.g. "if the is water too cold
for
linen, start heater"). Of course, if the robot is to learn
by
trial-and-error, it must somehow evaluate which actions were
successful.
We've entered the world of artificial intelligence (AI). AI is
concerned with reasoning, learning and making analogies in new
situations. The kinds of logic used are not always of the simple
yes
and no type, and learning paradigms abound. Sadly, I canÂt go
further into this for now. If you want to read more, see the
references [15, 16]. The point I wanted to make here is that
fractals may have something to do with (machine) intelligence.
Iterated systems (IS), such as computers, can show chaotic (fractal)
behavior.
Many questions arise. Here are few: Does the robotÂs state in
phase space move toward a strange attractor? What are the
consequences? For what purpose can we use the dynamics of
learning
systems if they are chaotic? Is there a danger in the low
predictability of chaotic systems? Engineers have just begun to
exploit nonlinear chaotic systems. Some chaotic systems can be
controlled by a chaotic signal and forced to express the desired
behavior [5]. Can chaotic systems be used to generate "creativity"
of robot artists? Or even for the automatic generation of unique
stories, films, architectural designs, virtual reality scenarios
or
other cultural artifacts? In BirkhoffÁs aesthetic theory, art is
defined as something not boring, but at the same time not too
surprising [12]. Fractals surely fit this simple criterion. So
they
may be useful for everyday design (and - in the hand of humans -
for
works of art).
"Using metaphor, we say that computers have senses and a
memory" said William Jovanovic [1]. In the dictionary [17],
intelligence is defined in two principal ways:
Meaning 1: consciousness, an intelligent entity (e.g. man),
intelligent minds or mind (e.g. cosmic intelligence), the act of
understanding, comprehension.
Meaning 2: mechanical thinking, which includes the ability to
learn
or to deal with new situations, the ability to apply knowledge to
manipulate one's environment or to think abstractly (as measured
by
tests).
I believe it is intelligence in the sense of meaning 1 that
creates mathematical ideas. It is a mind that looks at itself and
says "well, I am one 1; there is one of me 11, and this
description
has two parts 21 ...". However, prevalent theories insist
that even
human intelligence developed out of simple information-carrying
molecules (the DNA) via evolution of the genes in the contexts of
cell, organism and ecosystem. We do not know enough yet to
conclude
with absolute certainty that the intelligence of man is only that
of
a biological (molecular) machine. Molecules are subject to
quantum
processes. And we do not know whether consciousness is controlled
or
influenced by quantum processes [18, 19].
When the DNA is decoded, the chain of its four bases is
interpreted to produce proteins which can influence the
enviroment.
These proteins may be considered as a "meaning" of the
DNA. For
instance, enzymes, hair and nails are made of proteins. Seen
chemically, proteins are strings of amino acids which are folded
in
three dimensional space to give rise to the most complex forms.
The
folding is governed by the attraction between certain parts of
the
amino acids and the environment of the protein molecule.
The DNA is interpreted by ribosomes. Ribosomes are cell
particles that work with partial copies of the DNA to produce
proteins. Each triplet of DNA bases can be the code for an amino
acid or a control sign like "stop here". Again, there
is an iterated
system (the cell with its DNA in a biological context) that
produces
beautiful fractals [20].
Molecular scientists often use "folding" programs to
join
particular regions of a linear sequence into a 2-D pattern. Can
you
fold any of the longer strings of the Gleichniszahlenreihe, letÁs
say the 23rd iteration or so? Are there beautiful 2-D (or even 3-
D)
foldings of the Gleichniszahlenreihe? You can use the following
laws
(or a variation of them) as attracting force: - equal ciphers (or
elements) attract with a strength of 1 - a pair of mutually
attractive ciphers attracts stronger than single ciphers, a trio
more
than a pair and so on. - the "bonds" between the
ciphers cannot be
overstretched (else they would break up the "chemical bond")
-
different ciphers (or elements) repel each other.
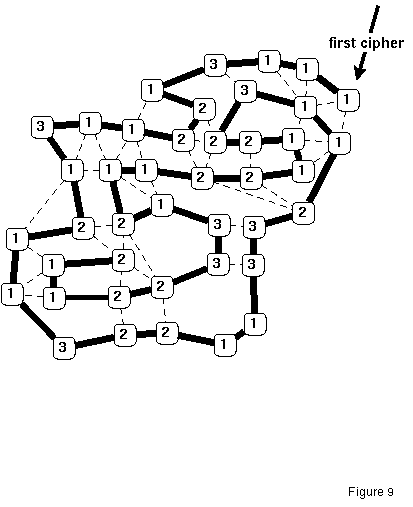
I've tried to fold the element 4Be, which is one of the two longest elements. The result is shown in figure 9. Thin dashed lines represent weak bonds between the ciphers. The fat lines denote the order of the string (strong bonds). Note the shorter strong bonds between equal ciphers (because of their attraction). The folding is essentially governed by the weak bonds. Can you find similar patterns for other cipher (or element) strings? I've shown a folding in the plane (two dimensions). What happens if three or more dimensions are allowed?
We wish to search for beautiful images by computer. Probably
you are using a computer monitor to watch the program-generated
images. Let's suppose the monitor has a resolution of 1000 pixels
(picture elements) horizontally and vertically, with 256 possible
colors for each pixel. How big is the picture space to be
traveled
by the beauty-seeking program? That's easy to compute from
combinatorics: 256 to the 1,000,000th power, which is roughly
equal
to 10^2,408,234. This is more than the square of a gigaplex,
which
Rudy Rucker defines as the sum of all possible thoughts of a man
[21]. Even if we settle for a low resolution black and white
monitor with 200*200 pixels we still have to cope with a picture
space of 2^40,000 or about 10^12,041. If 10 billion people
watched
for 80 years (without sleeping) a picture each second, this
enormous
effort could scan only 2.5*10^19 pictures.
Let's suppose, a "picture space of all fractal images"
can be
defined in some way. Because the number of fractal images may be
large, the time for "just looking at all the beautiful
fractal
images" is a lot longer than many lifetimes. This is true,
even if
you had a filter program to select for you "only the
beautiful ones,
and only one of each group of similar looking ones." If you
get
bored, you could modify your filter program to exclude "the
boring
ones" (and wait a little longer) or even trim your search
algorithm
to seek out realms in image space where "things are most
unsimilar
to things already discovered." Provided you have a "dissimilarity
measure," you may find something new. The ultimate limits,
of course,
are a) your picture-generating program, b) time and c) the number
of
pictures that a human can distinguish (as far as I know, this is
an
unknown number but probably very large, depending on the number
of
rods and cones on the retina and the number of neurons in the
visual
cortex).
What holds true for fractal images, is also true for sounds,
melodies and musical compositions, as other chapters in this book
illustrate. How do you in your quest for pattern and beauty
travel
this endless fractal ocean? You realize that you cannot see
everything in your lifetime - you cannot "have it all."
You must
omit an almost infinite number of things. Stanley Clarke sings
"so
life is just a game, and there's many ways to play, and all you
do
is choose"[22].
We can see now that the possibilities for Art are endless,
even in its classical dimensions (design, painting, sculpture,
architecture, poetry, literature, history, music, dance, drama
and
science). Any successful artist today can hardly avoid the
digitizing of his art in video images, CD recording or in files
of
design programs. In modern media, all is converted to signs or
symbols (numbers in most cases). Pythagoreans saw numbers and
their
proportions as the nature and essence of all things [23]. Some of
their discoveries were the harmonical laws in music and geometry
(e.
g. the Pythagorean theorem). Today, numbers form the basis for
the
recording, storing and retrieving of information (and a lot of
beautiful artistic compositions), regardless of the notion that
art
has a non-rational component that may not be computable at all.
All
of modern physics, genetics, "artificial life"[24, 25,
31] and
automata psychology (another term for artificial intelligence)
can
be seen as a quest for finding the ordering principles in nature
by
using mathematics as tool to operate on its models of nature or
even
generate its models.
What is the difference between a model and a metaphor? A
metaphor carries meaning beyond the obvious, therefore a metaphor
is
more than a theory. A metaphor can be a kind of guiding principle
for thought. One could explain a metaphor as a kind of high-level
analogy. For instance, the Gleichniszahlenreihe can be seen as a
curious mathematical object - as just another string-rewriting
system. However, we have already seen some of its metaphorical
qualities in the introduction.
Here are some exemplary metaphorical meanings of the
Gleichniszahlenreihe: - a metaphor for an iterated system
producing
a chaos of fractals - a mind looking at itself and bringing a
"world
with elements" into being - a meta-metaphor that shows what
a
metaphor is. A metaphor for a metaphor, for "jumping out of
the
system" and looking at it from the outside. - ...
The title was intentionally set in quotes to be distinguished
as an example (metaphor) for the view that there is something
like a
"world formula." Is it really possible to capture the
phenomena of
the physical and mental world in a finite set of mathematical
models? The evidence of the last centuries looks promising.
Scientific fields like celestial mechanics, quantum theory,
genetics
etc are good models in their domains. And I feel iterated systems
(IS, fractals) to be a most promising candidate for what the
Pythagoreans of today (physicists, geneticists and artificial
intelligence researchers) are after, with some caveats described
in
the next sections.
Look again at figure 1. Is it possible to iterate the matrix
in ways similar to figures 4 and 7? Which conceptual slippage [16]
is needed for such an operation? Can semantic nets [15] be used
for
prediction or scenarios?
Today the ellipse is the tool of the engineer and scientist,
and fractal mathematics are becoming more widely used, for
example
in solid state physics (quasicrystals, spin glasses) and in
control
theory (chaotic). French researchers have produced aerogels,
which
they claim the first totally fractal material of the world (down
to
the molecular level). Aerogels are known for their diverse fields
of
application from detectors to solar architecture [6].
Let me speculate about developments in the next century. The
fractal metaphor has now grown into a mental tool like the
ellipse
but is still in its youth (or infancy). This mental tool is
already
used not only by engineers [5] but by artists as well [8, 9].
Consumer products with more "artificial intelligence"
than exist
today will surely exhibit fractals in a variety of ways in their
programs and designs. Maybe there will not even be such a thing
as a
consumer product, as people order directly from a factory which
can
produce millions of variations.
If we look forward to the zeitgeist of the next century, it
might be strongly influenced by the fractal metaphor that is
already
so applicable and useful. Many natural-scientific and artistic
disciplines will re-discover what they have in common. One may be
tempted to believe that a unifying theory, based on IS, will
re-unite different sciences. Science will not only mean natural
science, but also the science of art, social science, mental
science
and others. Science may even mean something like religion in the
end, with some caveats described below.
As the classical architecture of the Romans and Greeks liked
circles and golden rectangles, as the baroque liked the ellipse,
so
the present likes the fractal metaphor. What will be the next
metaphor? Nonlinear dynamical systems were the "blind spot"
(or taboo
theme) that was touched on only slightly by the grand
mathematicians
of previous centuries. The metaphor "chaos and fractals"
also has a
blind spot. I have a vague feeling that fractals are already very
good,
but something is missing; I'll try to speculate wildly what this
may be:
It may be an object of mathematical theory that has more
complexity (or complexity of another kind) than fractals which is
applicable to wider fields of knowledge. Maybe another measure of
complexity will be found.
This object once found, it may lead to a paradigm not as
mechanistic as deterministic chaos, arriving at new "natural
laws"
(maybe a superset of quantum theory?) possibly undermining the
law
of cause and effect.
Then predictability of another kind might become applicable
(perhaps coupled to a "many worlds" theory, or
predicting specific
events in the far future, or backwards in time, or in light-year
distance). One might call this a "new paradigm" in
physics or "new
metaphor" in mathematics.
The art objects generated with this "new metaphor"
could look or
sound even nearer to life than those works of art based on
fractals. The new mathematical art possibly appears more "real"
and with an even better "ring of truth" than fractals
already
have.
The new metaphor may be accessible (or constructable) without
computers as we understand them today, enabling people to solve
problems that are (mechanically) incomputable today. A type of
computer beyond massive parallelism might evolve.
The usefulness of the new metaphor is demonstrable but not (or
seldom) provable by traditional mathematical tools.
Remember, we're past the event horizon - a place in spacetime
about which nothing can be known now; this is just my hunch.
Maybe
we will see the end of that kind of natural science which is
looking
for natural laws and the finite "model of the world."
Fractals
promise that such a model may exist, if we lower our expectations
for predictability. But the metaphor could carry us beyond itself
to the realization that "one metaphor fits all" is just
a metaphor
for the human quest for understanding, trying to fit infinity
into a
nutshell.
The voyage does not really end here. Rather, it has just begun.
To see a World in a Grain of Sand,
And a Heaven in a Wild Flower,
Hold Infinity in the palm of your hand,
And Eternity in an hour.
(William Blake 1757-1827) [1]
set
L 1/10 of your graphical display screen
r 1.3
alpha 30 degrees
beta 20 degrees
declare a string structure of adequate length (remember the rapid growth)
There are five signs to be iterated: "F", "[", "]", "+" and
"-". Start with the string "F" (the so-called "axiom" of the
L-system). The iteration rule is: "F" is expanded to "F[+F][-F]". All
other signs remain as they are.
You can interpret this string graphically in the following way
(imagine a drawing pen moving):
F draw a line (forward) of length L
[ store this position and divide L by r (r>1)
+ turn right by an angle alpha
- turn left by an angle beta
] return to the position previously stored and multiply L by r.
The factor r causes shortening of subsequent branches.
To compute the abundances of the elements (in table 1) the
following code has been used (in C-language). The code lines like
"new = old ..." can be taken directly from figure 4. There is a
vector abd that stores the old and new abundances. All initial
abundances are set to 1.0 . On my machine, I needed 330 iterations
before the growth factor gf converged. Here gf is computed from the
rarest element (33As) but you could use any element for the
computation. To avoid overflow, the abundances are normalized to 1.
0 . When you print the final abundances multiply by 1,000,000 to get
ppm (parts per million).
for (i=0; i<iterations; i++)
{
abd[1].new = abd[2].old + abd[58].old + abd[21].old + abd[73].old
+ abd[31].old + abd[40].old + abd[1].old;
abd[2].new = abd[3].old;
abd[3].new = abd[2].old + abd[4].old;
abd[4].new = abd[5].old;
abd[5].new = abd[6].old;
abd[6].new = abd[7].old;
abd[7].new = abd[8].old;
abd[8].new = abd[9].old;
abd[9].new = abd[10].old;
abd[10].new = abd[11].old;
abd[11].new = abd[12].old + abd[33].old;
abd[12].new = abd[13].old;
abd[13].new = abd[14].old;
abd[14].new = abd[15].old + abd[25].old;
abd[15].new = abd[16].old;
abd[16].new = abd[17].old;
abd[17].new = abd[18].old;
abd[18].new = abd[19].old;
abd[19].new = abd[20].old;
abd[20].new = abd[21].old + abd[69].old + abd[73].old + abd[75].old
+ 2*abd[31].old + abd[40].old + abd[4].old + abd[2].old
+ abd[44].old + abd[52].old + abd[62].old
+ abd[64].old + abd[58].old;
abd[21].new = abd[22].old;
abd[22].new = abd[23].old;
abd[23].new = abd[24].old;
abd[24].new = abd[25].old;
abd[25].new = abd[26].old;
abd[26].new = abd[27].old;
abd[27].new = abd[28].old + abd[69].old + abd[21].old
+ abd[64].old + abd[58].old;
abd[28].new = abd[29].old;
abd[29].new = abd[30].old;
abd[30].new = abd[31].old + abd[62].old + abd[28].old;
abd[31].new = abd[32].old;
abd[32].new = abd[33].old + abd[4].old + abd[75].old;
abd[33].new = abd[34].old;
abd[34].new = abd[35].old;
abd[35].new = abd[36].old;
abd[36].new = abd[37].old;
abd[37].new = abd[38].old;
abd[38].new = abd[39].old;
abd[39].new = abd[40].old;
abd[40].new = abd[41].old;
abd[41].new = abd[42].old;
abd[42].new = abd[43].old;
abd[43].new = abd[44].old + abd[40].old;
abd[44].new = abd[45].old;
abd[45].new = abd[46].old;
abd[46].new = abd[47].old;
abd[47].new = abd[48].old;
abd[48].new = abd[49].old;
abd[49].new = abd[50].old;
abd[50].new = abd[51].old;
abd[51].new = abd[52].old;
abd[52].new = abd[53].old;
abd[53].new = abd[54].old;
abd[54].new = abd[55].old;
abd[55].new = abd[56].old;
abd[56].new = abd[57].old;
abd[57].new = abd[58].old;
abd[58].new = abd[59].old;
abd[59].new = abd[60].old;
abd[60].new = abd[61].old;
abd[61].new = abd[62].old + abd[12].old + abd[51].old
+ abd[83].old + abd[68].old;
abd[62].new = abd[63].old;
abd[63].new = abd[64].old + abd[52].old + abd[44].old + abd[31].old;
abd[64].new = abd[65].old;
abd[65].new = abd[66].old;
abd[66].new = abd[67].old;
abd[67].new = abd[68].old + abd[15].old + abd[65].old
+ abd[45].old + abd[53].old
+ abd[21].old + abd[86].old + abd[32].old;
abd[68].new = abd[69].old + abd[41].old;
abd[69].new = abd[70].old;
abd[70].new = abd[71].old;
abd[71].new = abd[72].old;
abd[72].new = abd[73].old + abd[2].old;
abd[73].new = abd[74].old;
abd[74].new = abd[75].old + abd[73].old;
abd[75].new = abd[76].old;
abd[76].new = abd[77].old;
abd[77].new = abd[78].old;
abd[78].new = abd[79].old;
abd[79].new = abd[80].old;
abd[80].new = abd[81].old;
abd[81].new = abd[82].old;
abd[82].new = abd[83].old;
abd[83].new = abd[84].old;
abd[84].new = abd[85].old;
abd[85].new = abd[86].old;
abd[86].new = abd[87].old;
abd[87].new = abd[88].old;
abd[88].new = abd[89].old;
abd[89].new = abd[90].old + abd[31].old;
abd[90].new = abd[91].old;
abd[91].new = abd[92].old + abd[2].old + abd[21].old + abd[73].old;
abd[92].new = abd[39].old;
sum = 0.0; /* sum abundances for normalization to 1 */
for (j=1; j<=92; j++)
sum += abd[j].new;
if (((i+1)%10)==0) /* show every 10th growth factor */
{
gf = abd[33].new / abd[33].old; /* growth factor */
fprintf(stderr,"%d gf = %.16lf\n", i+1, gf);
}
for (j=1; j<=92; j++)
abd[j].old = abd[j].new / sum; /* normalization to 1 */
}
Conversion of an iterate of the GZR into a time-series-like
fractal graph. The abundances of ciphers in large iterates of the
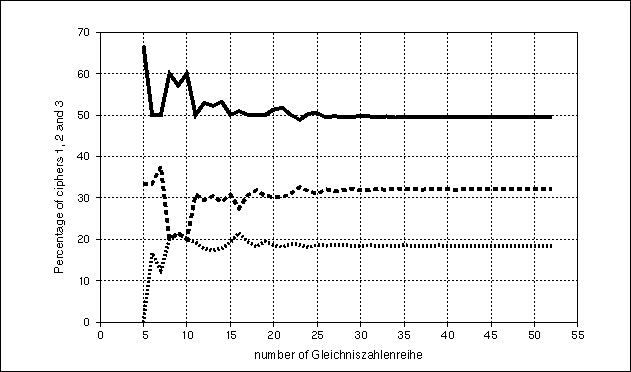
GZR are known to be about 49.5101% "1", 32.0352% "2" and 18.4547%
"3". In the following piece of code, ciphers are interpreted as "1"
= up, "2" = down, "3" horizontal (no change). The amounts of
increase or decrease are adjusted to give an approximately
horizontal line - at least to get an end value of the time-series
near the start value (0.0).
Read the next cipher from an iterate of the GZR
if the cipher is
{
1:value = value + 0.320352 / (0.320352 + 0.495101); /* up */
2: value = value - 0.495101 / (0.320352 + 0.495101); /* down */
3: /* 0.184547 do nothing */
}
Note: the cipher abundances of the GZR yield ( 0.495101 * 0.320352)
/ (0.184547 * 0.184547) = 4.65701, only 0.26 % smaller than
Feigenbaum's constant (about 4.66920) [11]. Can you explain this, or
is it just chance?
(listed in order of appearance)
[1] Smith, K. (1988,1990) Digital Quotations, Release (v28), NeXT
Computer, Inc.
[2] Ehrig, H., Kreowski, H.-J. and Rozenberg, G. (Eds.) (1991),
Graph Grammars and Their Application to Computer Science -
Proceedings of the 4th International Workshop, Bremen, Germany,
March 1990. Lecture Notes in Computer Science 532. Springer:
Berlin
Heidelberg
[3] Lindenmayer, A., and Prusinkiewicz, P. (1990) The Algorithmic
Beauty of Plants. Springer Verlag: Berlin, New York.
[4] Binnig, G. (1989) Aus dem Nichts - ueber die Kreativitaet von
Natur und Mensch. R.Piper GmbH & Co KG: Muenchen.
[5] Ditto, W.L. and Pecora, L.M. (1993), Mastering Chaos,
Scientific
American 8: 62
[6] Fricke, J. (1993), Aerogele - die leichte Alternative, Bild
der
Wissenschaft, 9: 78.
[7] Mayer-Kress, G. (1993),Chaos and Crises in International
Systems, Talk presented at SHAPE technology symposium on crisis
management, Mons, Belgium. Available via anonymous ftp from ftp.ncsa.
uiuc.edu in directory GlobalModels/Papers
[8] Pickover, C. (1992) Mit den Augen des Computers. Markt&Technik:
Mnchen. Also available as Computers and the Imagination, St.
Martin's Press: New York.
[9] Pickover, C. (1992) Mazes for the Mind: Computers and the
Unexpected. St. Martin's Press: New York.
[10] Mandelbrot, B.B. (1982) The Fractal Geometry of Nature. W.H.
Freeman and Company: San Francisco.
[11] Peitgen, H.-O., Juergens, H. and Saupe, D. (1992), Chaos and
Fractals - New Frontiers of Science. Springer Verlag: New York,
Berlin.
[12] Schroeder, M. (1991) Fractals, Chaos, Power Laws - Minutes
from
an Infinite Paradise. W.H.Freeman and Company: New York.
[13] Conway, J. (1987) The weird and wonderful chemistry of
audioactive decay. In : Cover, T. M., and Gopinath, B. (1987)
Open
Problems in Communications and Computation. Springer Verlag: New
York.
[14] Barnsley, M. (1988) Fractals Everywhere. Academic Press:
Boston, San Diego
[15] Hofstadter, D.R. (1980) Goedel, Escher, Bach: an Eternal
Golden
Braid. Random House / Vintage: New York
[16] Mitchell, M., (1993) Analogy-Making as Perception - A
Computer
Model. MIT Press: Cambridge, Mass.
[17] NeXT Computer, Inc., and Merriam-Webster Inc. (1988,1992)
Websters Ninth New Collegiate Dictionary and Websters Collegiate
Thesaurus. First Digital Edition, Version 3.0
[18] Penrose, R. (1989) The Emperor`s New Mind - Concerning
Computers, Minds and The Laws of Physics. Oxford University Press:
New York
[19] Eccles, J. (1989) Brain and Mind, Two or One? in: Blakemore,
C.
and Greenfield, S. Mindwaves. Basil Blackwell: London.
[20] Rensing, L. and Deutsch, A. (ca. 1990), Natur und Form -
Schoenheit und Gesetzmaessigkeiten rhythmischer Strukturen.
Zentraldruckerei der Universitaet Bremen, ISBN 3-88722-213-X
[21] Rucker, R. (1990) Der Ozean der Wahrheit - ueber die
logische
Tiefe der Welt. Fischer Logo: Frankfurt am Main.
[22] Clarke, S. (1976) School Days. Nemperor Records / Warner:
New
York.
[23] Simonyi, K. (1990) Kulturgeschichte der Physik. Verlag Harri
Deutsch: Thun, Frankfurt am Main
[24] Horgan, J. (1993) The Death of Proof, Scientific American 10:
72
[25] Langton, C.G., ed. (1989) Artificial Life - proceedings ...
Addison-Wesley: Redwood City
[26] Roessler, O.E., cited by Bruegge, P. (1993) Der Kult um das
Chaos, Der Spiegel 41, p.252
[27] Casti, J.L. (1993) Searching for Certainty - What Science
Can
Know About The Future. Abacus: London.
[28] Hilgemeier, M. (1986) Die Gleichniszahlen-Reihe, Bild der
Wissenschaft 12: 19.
[29] Cramer, F. (1993) Der Zeitbaum - Grundlegung einer
allgemeinen
Zeittheorie. Insel Verlag: Frankfurt am Main, Leipzig.
[30] Chatwin, B. (1992) Traumpfade. Fischer: Frankfurt am Main.
(German translation of The Songlines. Cape, London 1987.)
[31] Langton, C.G., Taylor, C., Farmer, J.D. and Rasmussen, S.,
eds.
(1992) Artificial Life II - proceedings ... Addison-Wesley:
Redwood
City
See also Henry Bottomley's Look and Say Java Script, Evolution of Conway's Elements and Seven Complete Orderings