I earlier produced a page
on Chebyshev's
inequality in both its original two-tailed version
and a one-tailed version. I produced another page on the difference
between the mean and mode in a unimodal distribution.
This page provides yet another proof
or two of the general one-tailed
version of Chebyshev's inequality (together with the associated median-mean inequality), and
what is almost a proof of the continuous unimodal
one-tailed version, which in turn gives various inequalities
including the mode-mean inequality, a median-mode inequality, and
a tighter median-mean inequality for the continuous unimodal case.
The reason for this page is
explained, with an alternative confirmation of the unimodal one-tailed
result. As ever, comments would
be welcome.
Henry
Bottomley. 2001
With proof of two lemmas, I now think the "almost a proof " is now actually a proof. The two-sided unimodal inequality needs just a little more work. HB. March/April 2002
If P[X-E(X)>=t] = 0 for given t>0 then clearly true, otherwise
let a=P[X-E(X)>=t], and
let b=E(X-E(X)|X-E(X)>=t) with b>=t>=0,
so E(X-E(X)|X-E(X)<t) = -ab/(1-a)
so Var(X) = a.E((X-E(X))2|X-E(X)>=t)+(1-a).E((X-E(X))2|X-E(X)>=t)
= a.E((X-E(X)-b)2|X-E(X)>=t) + a.b2 + (1-a).E((X-E(X)+ab/(1-a))2|X-E(X)>=t)
+ (1-a).(a.b/(1-a))2
>= a.b2+(1-a).a2.b2/(1-a)2
= a.b2/(1-a)
>= a.t2/(1-a)
so a = P[X-E(X)>=t] <= Var(X)/(Var(X)+t2)
Clearly equality is achieved for the first inequality in Var(X) if the probability is concentrated at the two points E(X)+b and E(X)-ab/(1-a), and for the second inequality in Var(X) when b=t, i.e. concentrated at the points E(X)+t and E(X)-at/(1-a).
With c>m and a probability density fuction for X of f(x), define:
g(x) and h(x) such that if x³c: g(x)=f(x) and h(x)=0, and if x<c: g(x)=0 and h(x)=f(x), so f(x)=g(x)+h(x)
a = P[X>=c] = òg(x).dx, so (1-a) = òh(x).dx
mg = òx.g(x).dx/a, so mg ³ c > m and mg-m ³ c-m > 0
mh = òx.h(x).dx/(1-a), so mh = m/(1-a)-a.mg/(1-a) £ m-a.(c-m)/(1-a) and m-mh ³ a.(c-m)/(1-a) > 0
sg2 = ò(x-mg)2.g(x).dx/a
sh2 = ò(x-mh)2.h(x).dx/(1-a)
so s2 = ò(x-m)2.g(x).dx
+ ò(x-m)2.h(x).dx
= ò(x-mg)2.g(x).dx
+ ò(mg-m)2.g(x).dx + ò(x-mh)2.h(x).dx
+ ò(m-mh)2.h(x).dx
= a.sg2 + a.(mg-m)2
+ (1-a).sh2 + (1-a).(m-mh)2
³ a.(mg-m)2 + (1-a).(m-mh)2
³ a.(c-m)2
+ (1-a).(a.(c-m)/(1-a))2
= a.(c-m)2/(1-a)
so a = òg(x).dx = P[X>=c] £ s2/(s2+(c-m)2)
with equality iff sg2 = sh2 = 0 and mg = c.
The median of a probability distribution cannot be more than 1 standard deviation from the mean, since:
P[X-E(X)>=sd(X)] <= Var(X)/(Var(X)+sd(X)2) = 1/2 and so no more than half of the probability can be more a standard deviation above the mean (and similarly by symmetry nor can more than half the probability be more a standard deviation below the mean).
There is some more discussion of this in A G McDowell's pages and on Usenet in alt.sci.math.probability and sci.stat.math.
Lemma 1
If X is a positive (or non-negative) continuous random variable with mean m and probability density function p(x) which is weakly monotonically decreasing in x>0, then:
What this says is that for a given mean, we minimise the second moment by having all the probability as close to 0 as possible, which happens with a uniform distribution.
Lemma 2
If X is a positive (or non-negative) continuous random variable with mean m and probability density function p(x) which either is weakly unimodal in x>0 with limx->0+p(x)>=h or is weakly monotonically decreasing in x>0, then:
(a) if 2mh<=1, then E(X2)>=(2/(3h2))*(mh-(1-2mh)*(1-sqrt(1-2mh)))
and Var(X)>=2m/h-(2/(3h2))*(1-(1-2mh)*sqrt(1-2mh)))-m2 ; or
(b) if 2mh>=1, then E(X2)>=4m2/3 and Var(X)>=m2/3
What this says is that for a given mean, we minimise the second moment by having all the probability as close to 0 as possible, which happens either (a) if the mean is small enough, with a uniform distribution followed by a point of as large positive probability as possible and as close to the mean as possible, or (b) if the mean is too large for that to be possible within the constraints, with a uniform distribution.
A proof of the two lemmas is below.
Main theorem
The unimodal one-tailed inequality is:
Case 0: If P[X-E(X)>=t] = 0 for given t>0 then clearly true,
otherwise let a = P[X-E(X)>=t], noting 0<a<1,
and b = E(X-E(X)|X-E(X)>=t), noting b>=t>=0,
and c = E((X-E(X))2|X-E(X)>=t), noting t2<=c<Var(X)/a
so E(X-E(X)|X-E(X)<t) = -ab/(1-a)
Case 1: If Mode(X)>=t+E(X)
(E(X)+t-X)|(X-E(X)<t) is a positive continuous random variable
with a weakly monotonically decreasing probability density
function f(y) (where y=E(X)+t-x) with mean ab/(1-a)+t
so (by Lemma 1) Var((E(X)+t-X)|(X-E(X)<t))>=(ab/(1-a)+t)2/3
But Var((E(X)+t-X)|(X-E(X)<t))=Var(X|(X-E(X)<t))=E((X-E(X)+ab/(1-a))2|X-E(X)>=t)
so Var(X) = a.E((X-E(X))2|X-E(X)>=t)+(1-a).E((X-E(X))2|X-E(X)>=t)
= a.E((X-E(X)-b)2|X-E(X)>=t)+a.b2+(1-a).E((X-E(X)+ab/(1-a))2|X-E(X)>=t)+(1-a).(a.b/(1-a))2
>= a.b2+(1-a).(ab/(1-a)+t)2/3+(1-a).(a.b/(1-a))2
>= a.t2+(1-a).(at/(1-a)+t)2/3+(1-a).(a.t/(1-a))2
= (3a+1).t2/(3(1-a))
i.e. P[X-E(X)>=t] <= (3.Var(X)-t2)/(3.Var(X)+3.t2))
= 1-4.t2/(3.(Var(X)+t2))
Case 2: If Mode(X)<t+E(X) then
(X-E(X)-t)|(X-E(X)>=t) is a non-negative continuous random
variable
with a weakly monotonically decreasing probability density
function f(y) (where y=x-E(X)-t) with mean b-t
so (by Lemma 1) E((X-E(X)-t)2|(X-E(X)>=t))>=(4/3)(b-t)2
and so limy->0+f(y)>=1/(2(b-t))
so (t-X+E(X))|(X-E(X)<t) is continuous random variable with mean (t+a(b-t))/(1-a) and probability density function g(z) (where z=t-x+E(x)) which is either weakly unimodal in x>0 and limz->0+g(x)>=a/(2(b-t)(1-a)) or weakly monotonically decreasing in x>0, so (by Lemma 2) either:
Case 2(a) if 2a(t+a(b-t))/(2(b-t)(1-a)2)<=1, i.e. if b>=t(1-a)/(1-2a), then
Var(X) = E((X-E(X)-t)2)-t2 >= (4/3).a.(b-t)2+(1-a).(2/(3h2)).(mh-(1-2mh).(1-sqrt(1-2mh)))-t2
where m=(t+a(b-t))/(1-a) and mh=a(t+a(b-t))/(2(b-t)(1-a)2)Let b=t.(1+1/(2.n-2.a.n-a.n2-a)) for some n, i.e. n=(1-a)/a-sqrt(((1-a)/a)2-t/(a.(b-t))-1)
then Var(X)>=t2.((4/3).(a+3.n2-2.a.n3-3.a.n2)/(2.n-2.a.n-a.n2-a)2-1)
This is minimised for n when n=(1-a)/a or when n=2
i.e. when b=t+a.t/(1-2.a) or when b=t+t/(4-9.a)So either Case 2(a)(i) when n=(1-a)/a,
in which case Var(X)>=t2/(3.(1-2a)2)
i.e. P[X-E(X)>=t] <= (1-t/sqrt(3.Var(X)))/2or Case 2(a)(ii) when n=2
in which case Var(X)>=t2.(4/(4-9a)-1)
i.e. P[X-E(X)>=t] <= 4.Var(X)/(9.(Var(X)+t2))
Case 2(b) if 2.a.(t+a.(b-t))/(2.(b-t).(1-a)2)>=1, i.e. if b<=t.(1-a)/(1-2a), then
E((t-X+E(X))2|(X-E(X)<t))>=(4/3).(t+a.(b-t))2/(1-a)2,
so Var(X)>=(4/3).a.(b-t)2+(4/3).(t+a.(b-t))2/(1-a)-t2 =(4.a.b2+t2-a.t2)/(3.(1-a))
so (since b>=t), Var(X)>=(3a+1).t2/(3.(1-a)) and we are back with the result at Case 1 of
P[X-E(X)>=t] <= (3.Var(X)-t2)/(3.Var(X)+3.t2)) = 1-4.t2/(3.(Var(X)+t2))
Comparing these three maximum values for P[X-E(X)>=t]:
(3.Var(X)-t2)/(3.Var(X)+3.t2));
(1-t/sqrt(3.Var(X)))/2; 4.Var(X)/(9.(Var(X)+t2));
the first and second are positive iff t2<3.Var(X)
in which case the first is greater than the second;
meanwhile, the first is greater than or equal to the third iff t2<=5*var(X)/3,
and so the result
P[X-E(X)>=t] <= Max{4.Var(X)/(9.(Var(X)+t2)),
(3.Var(X)-t2)/(3.Var(X)+3.t2))}
is proved.
Note that using these results we can put a limit on the difference between the median and mean of a continuous unimodal distribution by letting t<median(X)-E(X) (assuming w/o.l.o.g. that the median is higher than the mean) and reorganising the inequalities to give an expression for t in terms of Var(X) and a=1/2. This gives the result:
In addition the result of case 1 above has a non-negative probability only if t2<=3.Var(X) implying that for a continuous unimodal distribution:
Similarly, from case 2(a) it is possible to approach a probability of 1/2 in Case 2(a)(i), giving the result for a continuous unimodal distribution:
For the benefit of those without calculators, these continuous unimodal distribution inequalities could be written as:
|median(X)-E(X)| <= sd(X)*0.77459...
|mode(X)-E(X)| <= sd(X)*1.73205...
|mode(X)-median(X)| <= sd(X)*1.73205...
I produced this page to clarify some discussion with Tristrom Cooke at CSSIP in Australia who had also produced proofs of the general one-tailed version of Chebyshev's inequality in relation to discriminating between two distributions of point classes. He was also working on the unimodal one-tailed vesion and had noted that my result was consistent with his as he had already produced the function:
F(m,d,k) |
= |
(2*m-d)^2 ( m^2+
(2*k-d)*m + 3-d*k ) |
where m is the mode, k is the number of standard deviations from the mean, and d is another parameter of the distribution. Using MAPLE to optimise, he had obtained three allowable solutions:
| d = 0 , m = -1/k |
| d = (3/2)*(k^2+1)/k , m = k |
| d = 3*(sqrt(3) - 1/k) , m = 2*sqrt(3) - 3/k |
The code he was using calculated F(m,d,k) for each of these solutions, and then chose the maximum one. He noted that this seemed to correspond to my solution exactly (at least from the graphs).
It is indeed exactly the same as my result above,
rewritten as
P[X-E(X)>=k.sd(X)] <= Max{4/(9.(1+k2)),
(3-k2)/(3+3.k2))}
since the first solution produces 4/(9(1+k^2), i.e. case 2(a)(ii)
above,
the second [once 0/0 is avoided] produces (3-k^2)/(3+3*k^2) , i.e.
cases 1 and 2(b), and
the third produces (1-k/sqrt(3))/2, i.e. case 2(a)(i) which can
be ignored in the maximisation as it is less than case 1
when positive.
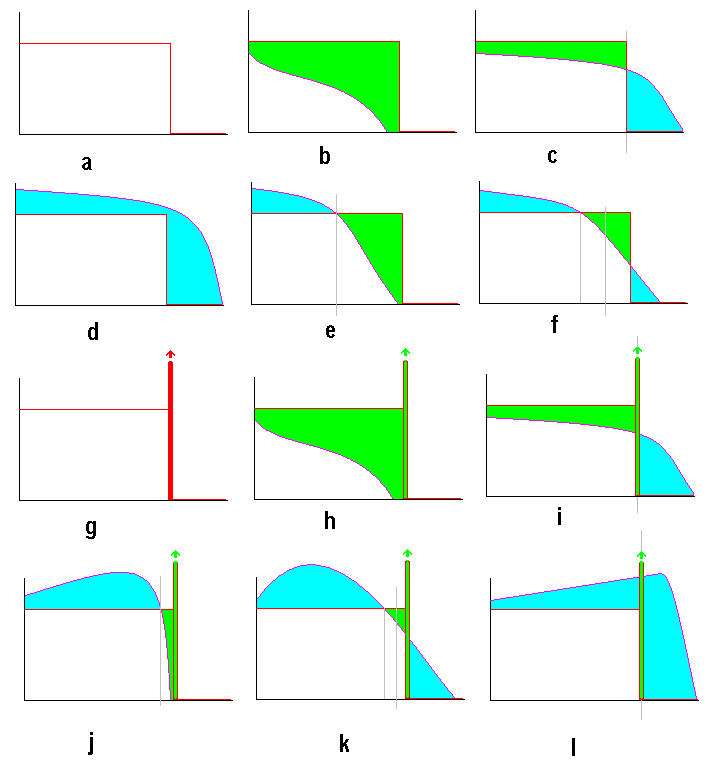
It has been pointed out to me that I did not provide a poof of the two lemmas above. What follows is largely essentially a graphical proof, comparing a general continuous random variable with a monotonically decreasing or unimodal probability density function which satisfies the given conditions against either a uniform distribution or a uniform distribution with a point of positive probability at one end.

Lemma 1: If X
is a positive (or non-negative) continuous random variable with
mean m and probability density function p(x) which is weakly
monotonically decreasing in x>0, then:
E(X2)>=(4/3)*m2,
Var(X)>=m2/3, and
limx->0+p(x)>=1/(2m).
We will compare a general p(x) satisfing this with the uniform
u(x) which is:
u(x)=1/(2m) if 0<x<2m and u(x)=0 if x<0 or x>2m,
so u(x) satisfies the conditions with equalities and is
illustrated in (a) above.
Looking at (b) it is not possible that p(x)<=u(x) for all x [unless p(x)=u(x) almost always], since such a p(x) would give a total probability less than 1 [the difference being the green area].
Looking at (c) it is not possible that p(x) can be less than 1/(2m) for all positive x, since the first moment of p(x) about a line at 2m would not be the same as the first moment of u(x) [all the blue area is to the right of the line and all the green to the left], which it must be if they are to have equal means.
This proves that limx->0+p(x)>=1/(2m).
Looking at (d) it is not possible that p(x)>=u(x) for all x [unless p(x)=u(x) almost always], since such a p(x) would give a total probability graeter than 1 [the difference being the blue area].
So there is at least one value z at which p(x) and u(x) are equal (or at least cross) with 0<z<2m
Looking at (e) it is not possible that p(x)=0 for all x>=2m [unless p(x)=u(x) almost always], since the first moment of p(x) about a line at z would not be the same as the first moment of u(x) [all the blue area is to the left of the line and all the green to the right], which it must be if they are to have equal means.
So the position must in fact be essentially like (f), with p(x) and u(x) equal or crossing at z (<2m) [and the total blue area must be equal to the total green area]. Considering moments about a line at (z+2m)/2, the first moments of p(x) and u(x) must be the same [and similarly of the blue and green areas] since their means are the same. But the second moment of p(x) here must be greater than or equal to that of u(x) [since all of the green area is closer to the line than any of the blue area] and so second moments of p(x) about other lines must be greater than or equal to those of u(x), i.e. E(X2)>=(4/3)*m2, Var(X)>=m2/3 [with equality only if the blue and green areas are both zero, i.e. if p(x)=u(x) almost always.]
Lemma 2: If X
is a positive (or non-negative) continuous random variable with
mean m and probability density function p(x) which either is
weakly unimodal in x>0 with limx->0+p(x)>=h
or is weakly monotonically decreasing in x>0, then:
if 2mh<=1, then E(X2)>=(2/(3h2))*(mh-(1-2mh)*(1-sqrt(1-2mh)))
and
Var(X)>=2m/h-(2/(3h2))*(1-(1-2mh)*sqrt(1-2mh)))-m2
; or
if 2mh>=1, then E(X2)>=4m2/3
and Var(X)>=m2/3
Looking at 2mh>=1 first, we essentially repeat the steps in the proof for Lemma 1, using the same u(x).
If p(x) is weakly monotonically decreasing,
then from (b) and (c)
we can see again that limx->0+p(x)>=1/(2m)
while if p(x) is weakly unimodal then we already know limx->0+p(x)>=h>=1/(2m).
Diagrams (d), (e) and (f)
and the associated aguements from the proof of Lemma 1 apply
whether (p) is weakly monotonically decreasing or weakly
monotonically decreasing and so we obtain the same result:
E(X2)>=(4/3)*m2,
Var(X)>=m2/3 [with
equality only if the blue and green areas are both zero, i.e. if
p(x)=u(x) almost always.]
Now looking at 2mh<=1, the proof is
similar to Lemma 1, but instead we compare p(x) against v(x)
where
v(x)=h if 0<x<w, v(x)=0 if x<0 or x>w,
and a point of positive probability Prob(X=w)=sqrt(1-2mh),
where w=(1-sqrt(1-2mh))/h [and noting that m<w<=2m],
as illustrated in (g) with the positive
probability counting as if it was an area
and so v(x) satisfies the conditions with equalities .
For p(x) weakly monotonically decreasing, diagrams (h)
and (i) are similar to (b) and (c)
leading to the conclusion that limx->0+p(x)>=h,
something we already know if p(x) is weakly unimodal.
Diagram (j) is similar to (e) and again enables us to conclude that it is not possible that p(x)=0 for all x>=2m [unless p(x)=v(x) almost always].
Ithink this should be
Diagram (j) is similar to (e) and again enables us to conclude that it is not possible that p(x)=0 for all x>=(1-sqrt(1-2mh))/h [unless p(x)=v(x) almost always].
That leaves (k) and (l) as
possibilities which can actually occur, with with p(x) and v(x)
equal or crossing at z (with z<w in (k) and z=w
in (l)) [and the total blue area must be equal
to the total green area, with the positive probability counted as
a green area]. Again considering moments about a line at (z+w)/2,
the first moments of p(x) and v(x) must be the same [and
similarly of the blue and green areas] since their means are the
same. But the second moment of p(x) here must be greater than or
equal to that of v(x) [since all of the green area is closer to
the line than any of the blue area] and so second moments of p(x)
about other lines must be greater than or equal to those of v(x),
i.e. E(X2)>=(1-sqrt(1-2mh))*w2/3+sqrt(1-2mh)*w2
=(2/(3h2))*(mh-(1-2mh)*(1-sqrt(1-2mh)))
and Var(X)=E(X2)-m2>=2m/h-(2/(3h2))*(1-(1-2mh)^(3/2)))-m2
[with equality only if the blue and green areas are both zero, i.e.
if p(x)=v(x) almost always.]
Diagrams (j), (k) and (l) show unimodal examples for p(x) but precisely the same arguments apply if it is monotonically decreasing. While (l) looks like (d), the point of positive probability enables p(x) and v(x) to represent probability distributions simultaneously in (l) while its absense prevents this in (d).
In my view that is all that is required to complete the proof of the one tailed unimodal case.
Henry Bottomley March 2002 (and minor corrections to the proof of Lemma 2 in November 2002)
Here is a sketch of why this can be shown to be true. It is some way away from being a proof.
As before we shall minimise the variance to demonstrate the inequality for given P[|X-E(X)|>=t].
The key initial step is to show that for any unimodal distribution, there is another (consisting of a point of positive probability combined with a uniform distribution of the rest of the probability which has the same value for P[|X-E(X)|>=t] and an equal or lower variance. This is illustrated in the charts below
There are two possibilities: either the mode is inside the interval (E(X)-t,E(X)+t) such as the example shown at (j); or it outside, such as the example shown at (k).
If the mode is inside and has a probability density function p(x),
then we can equally well consider the function:
g(x)=(p(x)+p(2*E(X)-x)/2,
i.e. the average of the original pdf and its reflection about E(X).
This will have the same value for P[|X-E(X)|>=t] and the same
variance, but is symmetric about E(X). We then proceed to
construct from g(x) a new distribution, which is also symmetric
about E(X), has a uniform distribution except for a point of
positive probability at E(X), has the same value for P[|X-E(X)|>=t]
and a lower (or equal variance). An example is illustrated at (l).
If the mode is outside, for example at or above E(X)+t, then we proceed to construct from p(x) a new distribution with a point of positive probability at E(X)+t and with the remainder of the probability distributed uniformly in an interval whose top end is E(X)+t, which has the same value for P[|X-E(X)|>=t] and a lower (or equal variance). An example is illustrated at (m).
Depending on the initial p(x), the first of these methods for a mode inside (E(X)-t,E(X)+t) may not in fact be possible. Having g(x) bimodal does not necessarily make it impossible. Not even having the value of g(E(X)) below the height of the uniform distribution necessarily makes it impossible, as shown at (n). But there can be cases where the mode of p(x) is just below E(X)+t or just above E(X)-t and the probability density in most of the rest of (E(X)-t,E(X)+t) is extremely low, where it does become impossible to do the suggested operation, with an example of the resulting g(x) at (o) which suggests that E(X) may need to have an (impossible) point of negative probability. In such a case, it will instead be possible to act in the same way as if the mode was outside (E(X)-t,E(X)+t) and proceed as illustrated at (m) to construct from p(x) a new distribution with a point of positive probability at E(X)+t (or E(X)-t) and with the remainder of the probability distributed uniformly in an interval with that as an end point.
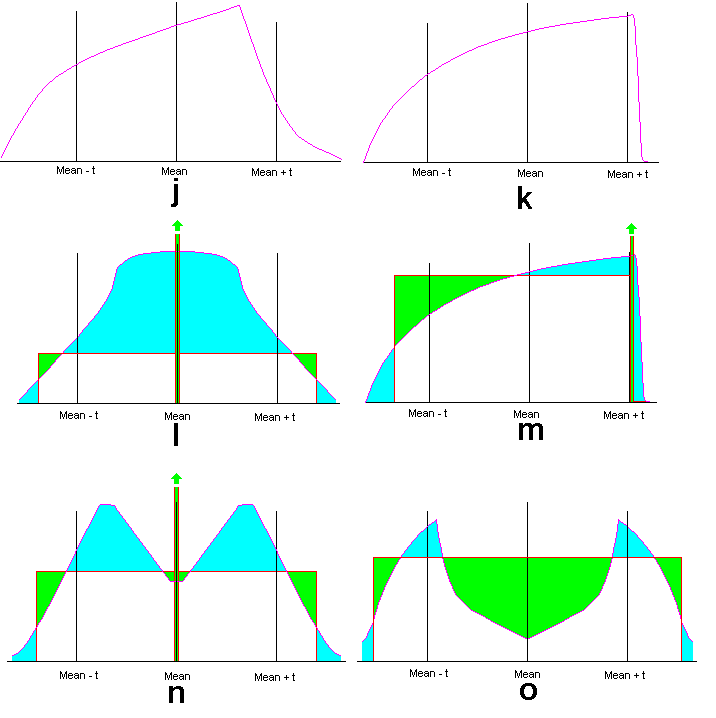
So we have two alternatives: a uniform distribution with a
point of positive probability:
either (i) in the middle
or (ii) at one end at E(X)+t, or with an
equivalent treatment if at E(X)-t.
In both cases we will take the point of positive probability
as being 1-q, with the remaining q being unifomly distributed
with a height h over a width q/h.
Clearly 0<=q<=1, and there is no need to go further if q/h<2t
since P[|X-E(X)|>=t] would then be 0.
In (i), P[|X-E(X)|>=t]=q-h*2t.
Setting this equal to a gives h=(q-a)/(2t).
Meanwhile the variance of the distribution is q^3/(12*h^2),
i.e. t^2*q^3/(3*(q-a)^2).
For given a, this is minimised when q=3a with a minimum value of
the variance of 9a*t^2/4 providing a<=1/3,
or if a>1/3 then when q=1 with a minimum value of the variance
of t^2/(3*(1-a)^2).
The first of these gives P[|X-E(X)|>=t] <= 4.Var(X)/(9.t2),
while the second gives P[|X-E(X)|>=t] <= 1-t/(sqrt(3*Var(X)))
where the first applies if t2>=4.Var(X)/3,
and the second if 0<t2<=4.Var(X)/3
In (ii), P[|X-E(X)|>=t]=(1-q)+(q-h*2t)=1-h*2t.
Setting this equal to a gives h=(1-a)/(2t).
For the mean to be E(X), we need q^2/(2h)-tq+h*t^2/2=t-tq+h*t^2/2,
i.e. q^2=1-a.
Meanwhile the variance of the distribution is t^2-t*q^2/h+q^3/(3h^2),
i.e. t^2*(4/(3*sqrt(1-a))-1) as a minimum
variance for a distribution which can be treated as in (ii).
This gives P[|X-E(X)|>=t] <= 1-(4.t2/(3.(Var(X)+t2)))2
Since this must be non-negative, we must have t2<=3.Var(X)
which is not a surprise given the mean-mode inequality above.
So to combining these results for potential minimum values
requires considering the highest minimum value of P[|X-E(X)|>=t]
for each possible value of t^2/Var(X). This gives:
if t^2/Var(X)>3 then P[|X-E(X)|>=t] <= 4.Var(X)/(9.t2);
if 4/3<t^2/Var(X)<=3 then P[|X-E(X)|>=t] <= Max{4.Var(X)/(9.t2),1-(4.t2/(3.(Var(X)+t2)))2};
if t^2/Var(X)<4/3 then P[|X-E(X)|>=t] <= Max{1-t/(sqrt(3*Var(X))),1-(4.t2/(3.(Var(X)+t2)))2}.
In the second of these, the two limits cross at t^2/Var(X)=C,
where C is the largest root of 7.x3-14.x2-x+4=0,
about 1.91930...; while in the third, the second limit is higher
than the first.
We can therefore simplify the result to:
If t>=B.sd(X) then P[|X-E(X)|>=t] <= 4.Var(X)/(9.t2)
If t<=B.sd(X) then P[|X-E(X)|>=t] <= 1-(4.t2/(3.(Var(X)+t2)))2
where B is the largest root of 7.x6-14.x4-x2+4=0,
about 1.38539...
which is what we were aiming to show.
HB April 2002
return to top Henry Bottomley's home page
Chebyshev's inequality Mode-Mean
inequality
Statistics Jokes Mean-Median-Mode-Standard Deviation