
Somebody was searching for triangles with the same area and perimeter. They found my page on calculating the area of a triangle, which probably did not help on this question, so here are some thoughts which could.
Such triangles exist. Consider the Heronian triangles (integer sides and areas) with sides 17,25,28 and 20,21,29: they both have perimeters of 70 and areas of 210. Or the triangles 24,37,37 and 25,34,39 and 29,29,40: these three have perimeters of 98 and areas of 420.

Michael Somos's list throws up some more examples; Mohammed Aassila has shown there are an infinite number of Heronian duplicates (though it might be difficult to access the article). But I am more interested in the general case, where the sides are positive real numbers. So here is the main fact demonstrated below for sensible cases:
There are an infinite number of triangles with a given perimeter and area.
Here "sensible cases" means that for a given area, the perimeter is large enough for there to be at least one non-equilateral triangle meeting the conditions. This turns out to mean that the square of the perimeter must be more than the area times the square-root of 432; note that 432=16*27.
The easiest way to show this is to use Heron's formula for the area of a triangle with semi-perimeter s and with sides x, y and z:
A = √( s (s-x) (s-y) (s-z) )
We have perimeter p = 2s, and clearly s-z = x+y-s, so this becomes:
16A2 = p (p-2x) (p-2y) (2x+2y-p)
or
y2 - (p-x)y +4A2/(p (p-2x) ) +p2/4 -xp/2 =0
which gives
y = (p-x)/2 +/- √( x2/4 - 4A2/(p(p-2x)) )
and z is the same but with the opposite sign for the square-root, i.e.
z = (p-x)/2 -/+ √( x2/4 - 4A2/(p(p-2x)) )
so we can also conclude that for given A and p, x determines y and z; i.e.:
Any triangles with the same perimeter and area and with one side the same are congruent.
This is no surprise. Imagine trying to identify all triangles with a given edge and a known perimeter. Possible positions for the third vertex lie on an ellipse with the vertices of the given edge as its foci and the length of its major axis being the difference between the perimeter and the given edge.

The area of a triangle is half of the product of the base and the perpendicular height, so given the base and the area, the height is fixed. But there are only four possible triangles with this height; they are reflections of each other in the axes of the ellipse and so congruent.
For all this to make sense, we need the number ( x2/4 - 4A2/(p(p-2x)) ) being square-rooted earlier to be non-negative; when it is zero we will have y=z and the triangle will be isosceles. So we need
p (p-2x) x2 / 16 >= A2
For given positive p, the left hand side is a cubic in x: with roots at x=p/2 and at x=0 (twice), positive for negative x, positive when 0<x<p/2, and negative when x>p/2, with turning points at x=0 and x=p/3, so A2 achieves its maximum possible value for positive x when x=p/3 in which case it is p4/432.
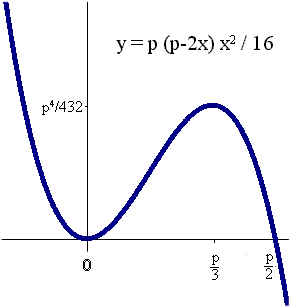
Clearly any horizontal line between zero and p4/432 intersects this cubic three times.
So providing that p2>A√432 as mentioned earlier, there will be a subinterval of [0,p/2] for x which will allow y and z to be calculated. At the extremes of the subinterval and only there the square root will vanish, leaving y and z equal to each other: in other words the associated triangles are isosceles. Incidentally we have shown that:
The triangle which maximises area for a given perimeter is the equilateral triangle with each side a third of the perimeter; the area is then p2/√432.
And for sensible cases
There are exactly two isosceles triangles with given perimeter and area.
Solving cubic equations is not particular attractive but for those who care, the highest possible positive value for x given p and A is
(p/3) (1/2 + cos( acos(1-(864*A2/p4))/3 ) )
while the lowest is
(p/3) (1/2 + cos( acos(1-(864*A2/p4))/3 -2π/3) )
(the third, negative, root is the same as the lower positive root but with the sign before 2π/3 reversed). As an example from earlier, if p=98 and A=420 then the lowest possible positive value for x is 24 and the highest is 40 (the negative root is -15).
Going back to the original formula for the relationship between two sides of the triangle x and y for given perimeter p and area A, we can draw this relationship as a set of curves. The chart below looks like a set of contours where p is fixed and A varies between the curves. The scale does not matter.
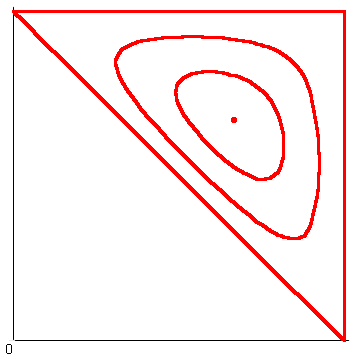
Take the inner curve for example, which was based on a perimeter of 98 and area of 420. Choosing a particular value for x for the length of one of the sides enables two possible values for y to be read off the chart – one of these can taken as the second side and the other the third. But similarly a particular value of y allows two values of x to be read of the chart. So the curve need to be symmetric in the line y=x. But there is even more symmetry involved. Recalling the 25,34,39 Heronian triangle, not only do the points (25,34) and (25,39) lie on the curve, but so do (34,25) and (39,25) and also (34,39) and (39,34). We also know some other points on this curve: at the extreme left we have (24,37) and at the extreme right we have (40,29); by symmetry we have (37,24) at the bottom and (29,40) at the top and we also have (29,29) and (37,37).
But this graph is not quite satisfactory given the six possible permutations of the tree sides of a triangle. An alternative would be to redraw the contours based on three axes of an equilateral triangle with its six-fold symmetry, taking the three co-ordinates of a point as its perpendicular distances to each of the three axes. Since each edge cannot be more than half the perimeter, we would be restricted to the middle quarter of the axes' triangle. The graph above would then look like this:
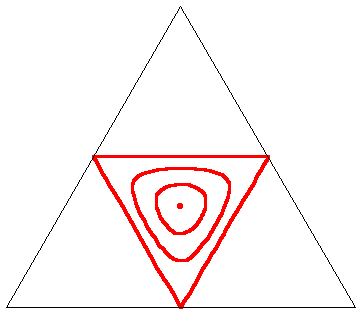
Henry Bottomley May 2006.
Some similar and related points can be found in Angles, Area, and Perimeter Caught in a Cubic by George Baloglou and Michel Helfgott, published in Forum Geometricorum, Volume 8 (2008) 13–25.
Circumnavigating a cube and a tetrahedron